题目传送门

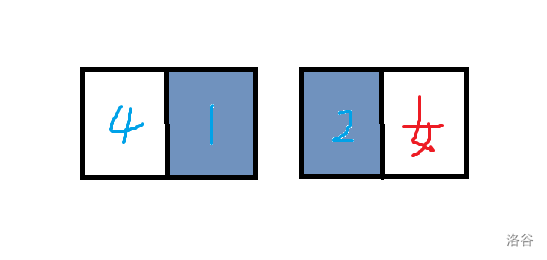
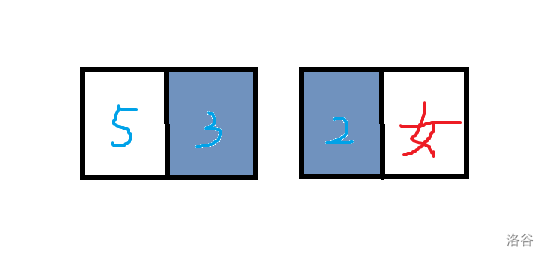
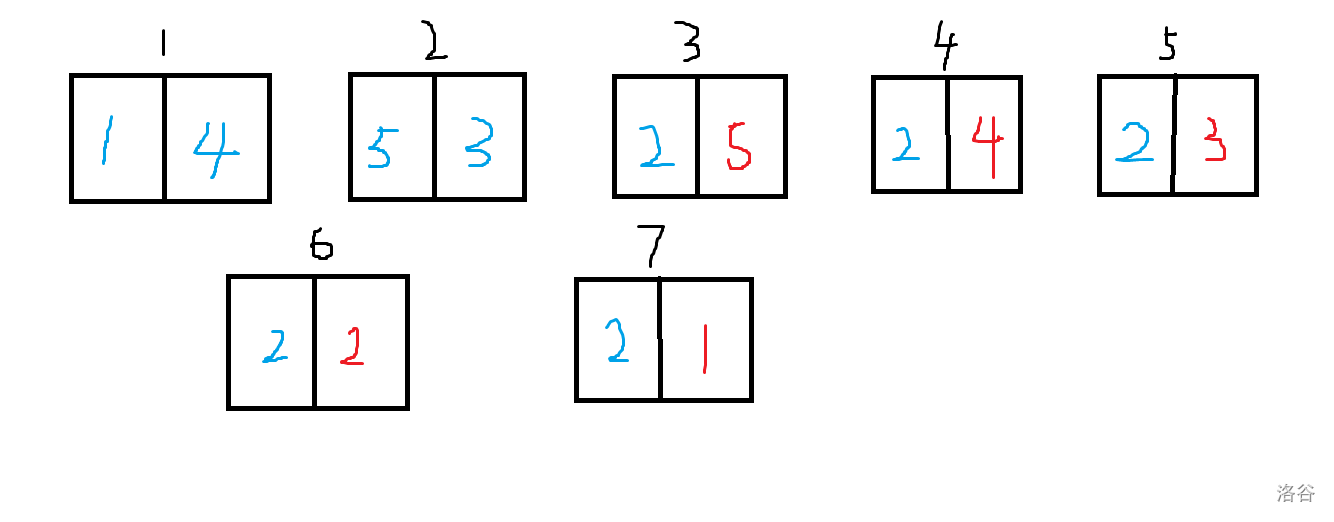
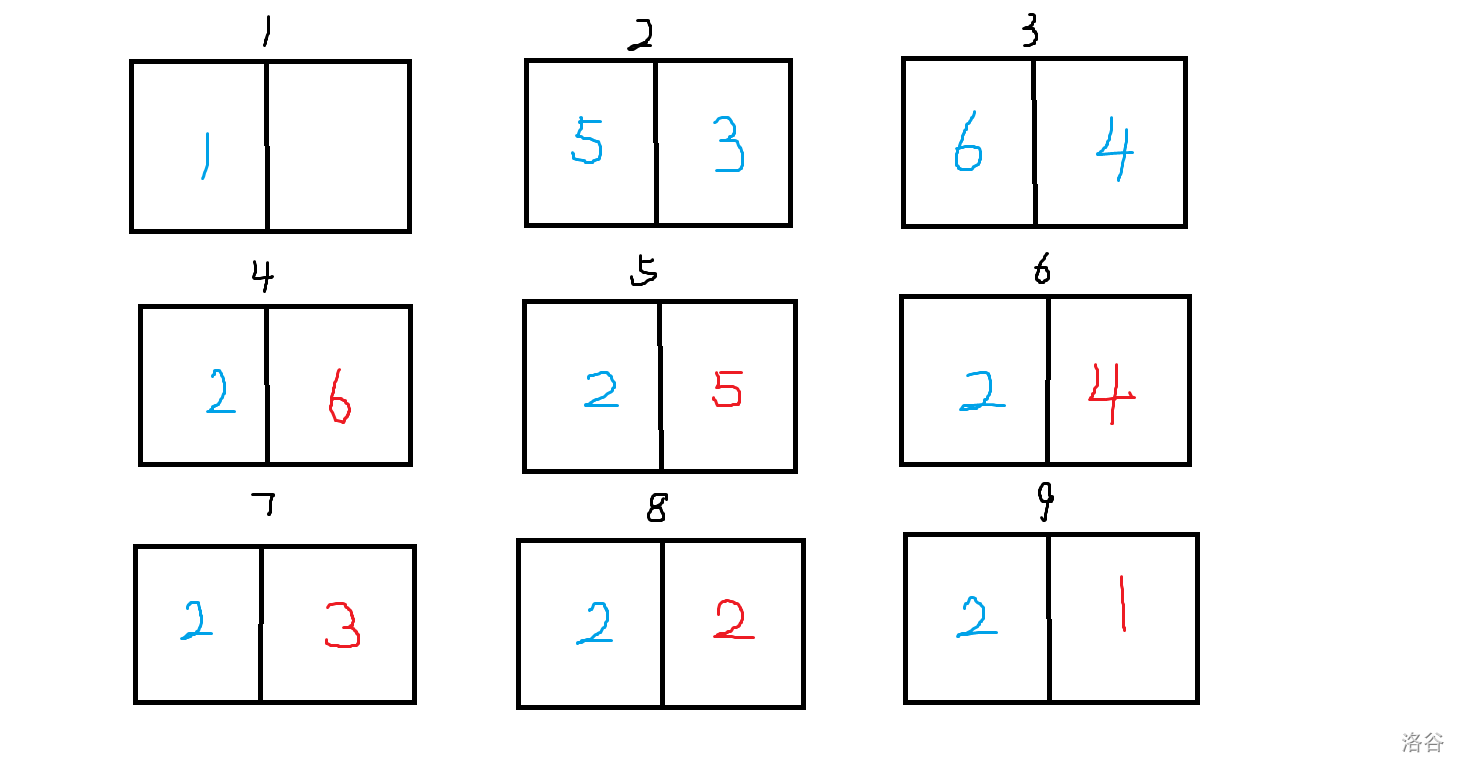
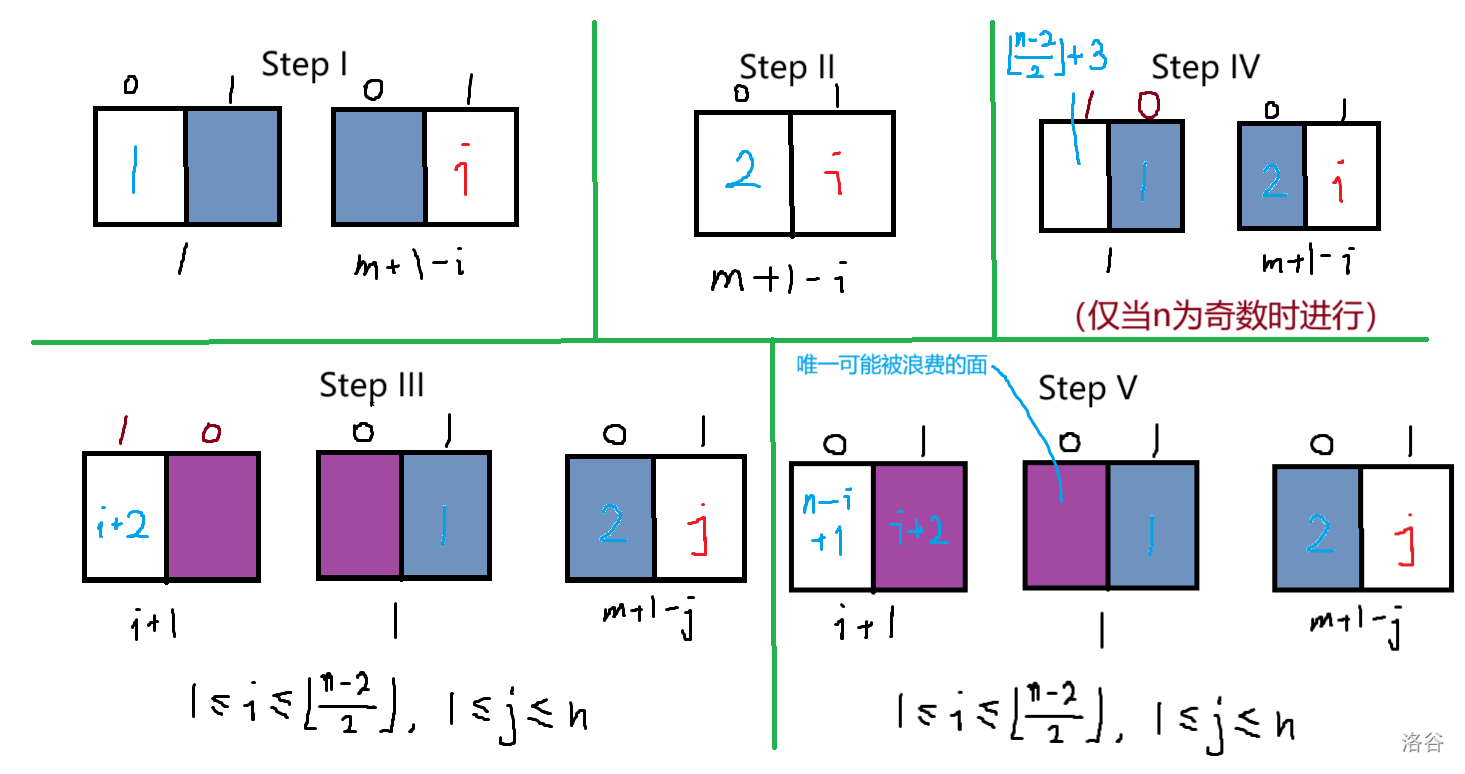
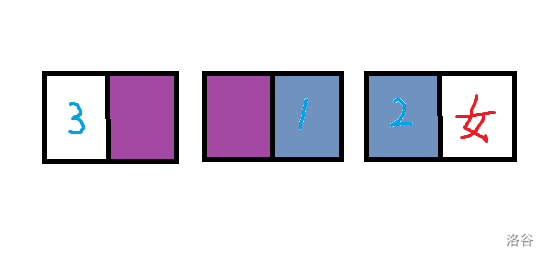题目描述

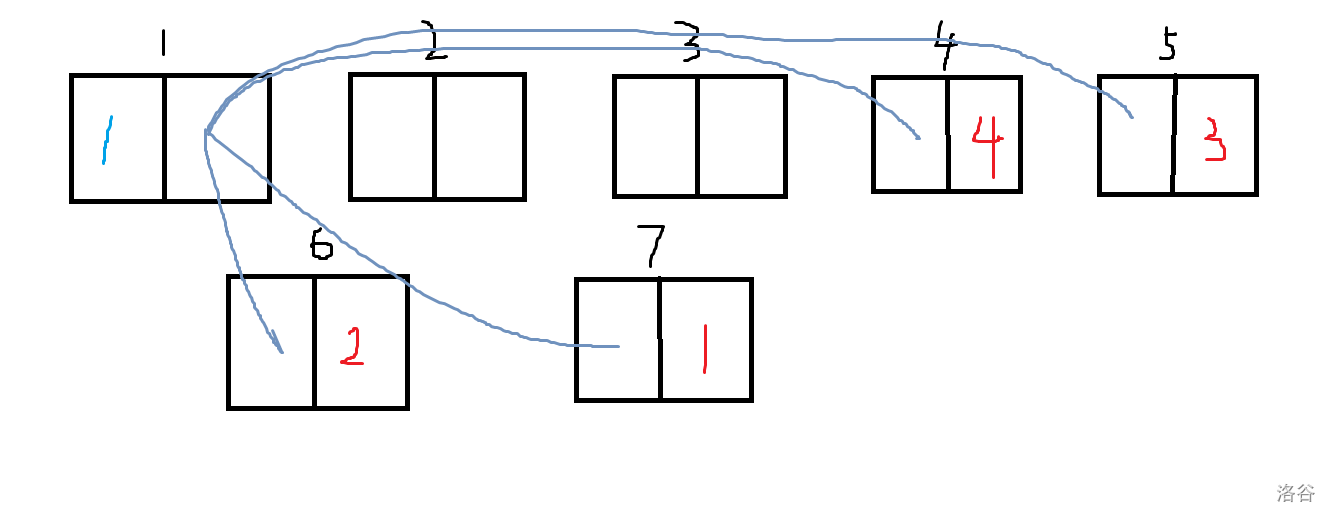
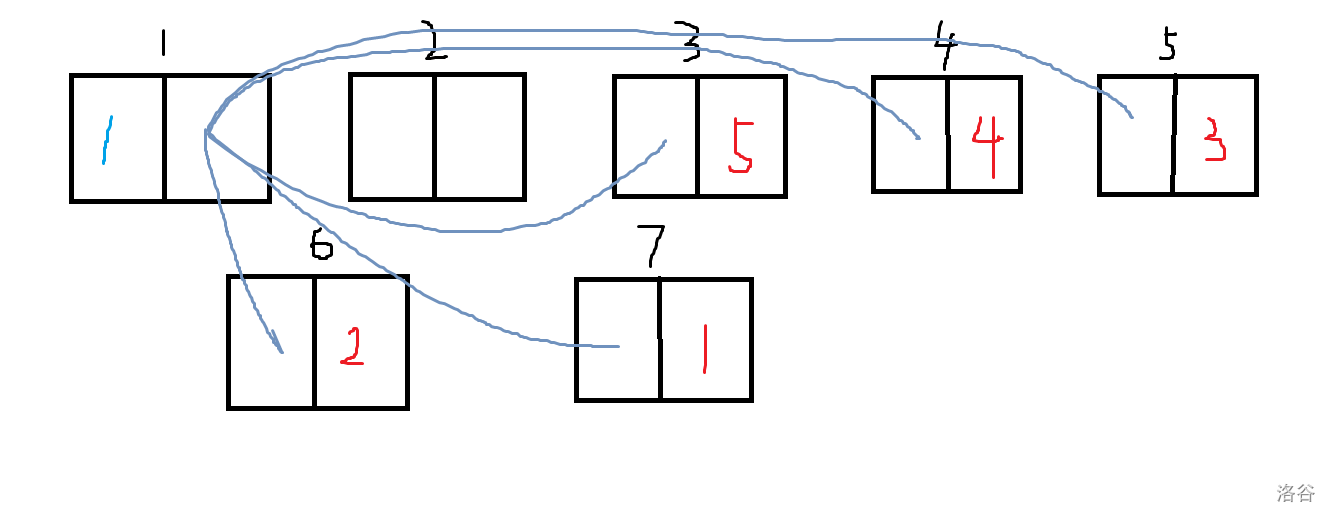
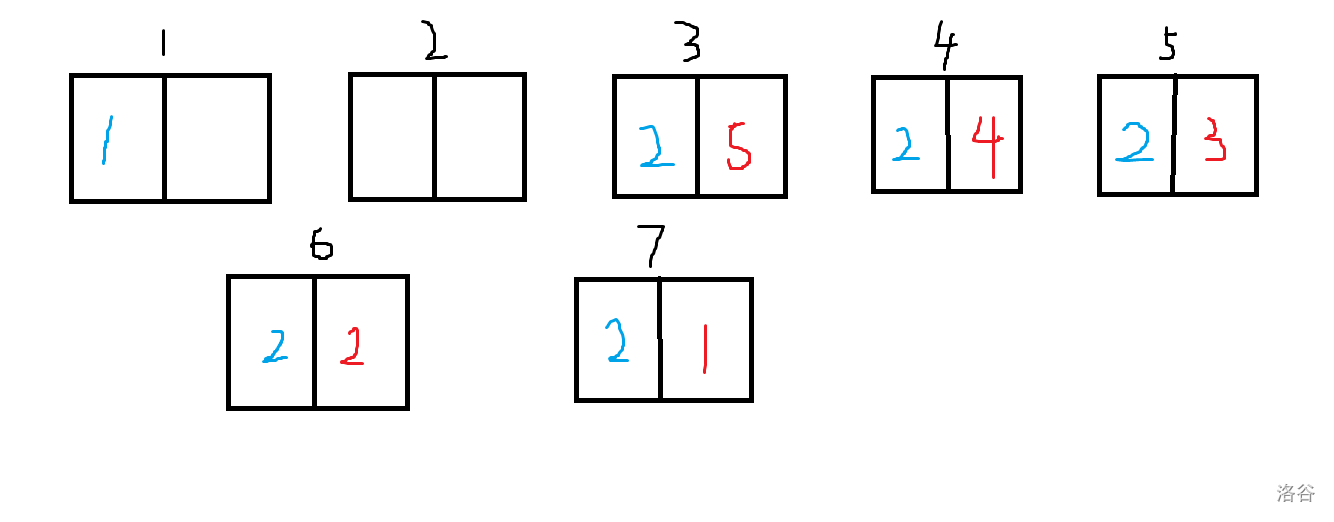
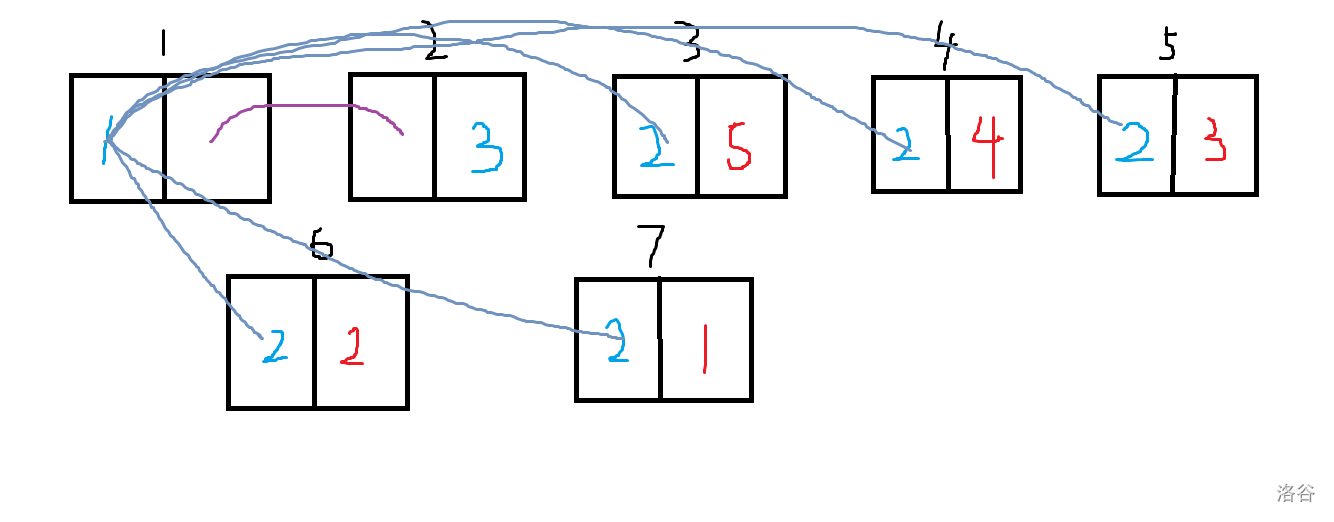
你面前的黑板上写了 $[1,n]$ 中的所有正整数各一个。你的手里有一个计数器 $cnt$，初始为 $0$。

每次，你会选择黑板上最小的数 $x$（若有多个相同，只选择其中一个），并执行如下操作：

• 如果 $x=1$，那么直接将其从黑板上擦除；
• 否则，将 $cnt$ 加上 $(x\bmod 2)$ 的值，并擦除 $x$，然后写上两个 $\lfloor\frac{x}{2}\rfloor$。

请求出：当黑板上的数字全部被擦除时，$cnt$ 的值。

数据范围：$1\le n\le 10^9$。

解析

Update on 2025/8/11：同机房同学给出了一种极简做法，写在这里：

开始时，所有数的值之和为 $\displaystyle\sum_{k=1}^{n}k=\frac{n(n+1)}{2}$。

记 $\text{highbit}(i)$ 为 $i$ 的二进制最高位的值，则 $Ans=\displaystyle\frac{n(n+1)}{2}-\sum_{i=1}^{n}\text{highbit}(i)$。

显然 $\displaystyle\sum_{i=1}^{n}\text{highbit}(i)=\sum_{j\ge 0,2^j\le n}\Big(\min(2^j,n-2^j\color{red}{+1})\times 2^j\Big)$。

然后算这个式子就可以了，时间复杂度 $\mathcal{O}(\log n)$。

Part 1

我们显然不能直接暴力枚举。

定义“初始数字”为在所有操作开始前，写在黑板上的数字。我们注意到，处理时，任意两个初始数字不互相影响。也就是说，我们可以假设开始前黑板上只有一个数字 $i$（$1\le i\le n$），记此时最终的 $cnt$ 为 $cnt_i$，则 $Ans=\displaystyle\sum_{i=1}^{n}cnt_i$。

Part 2

我们思考一下求 $cnt_i$ 的过程到底是在干什么。设当前 $i=x$。

我们实际在干这么一件事：

• 维护一个权值 $w$，初始 $w=2^0$（即 $1$）。
• 重复执行如下操作：
• • 如果 $x=1$，那么结束整个流程；
• • 否则，$cnt\leftarrow cnt+(x\bmod 2)\times w$，然后 $x\leftarrow\lfloor\frac{x}{2}\rfloor$，$w\leftarrow w\times 2$（也就是将 $x$ 右移一位，将 $w$ 左移一位）。

容易发现，在第 $j$ 次操作中，$w=2^{j-1}$，$(x\bmod 2)$ 的值对应初始 $x$ 中 $2^{j-1}$ 位置的值。这个结论在正解中有用，先记着。

这样我们就有时间复杂度 $\mathcal{O}(n\log n)$ 的做法了，但这还不够。

Part 3

我们把上面的过程改一下，不是枚举数而是枚举二进制位。

根据 Part 2 中我们得到的结论，我们容易得到：$2^{j-1}$ 位置对最终答案的贡献为 $(cnt_A-cnt_B)\times 2^{j-1}$，其中：

• $cnt_A$ 是 $[1,n]$ 中的所有整数中，二进制位中 $2^{j-1}$ 位置为 $1$ 的数的个数；
• $cnt_B$ 是 $[1,n]$ 中的所有整数中，以 $2^{j-1}$ 为二进制最高位的数的个数。

如何快速求出 $cnt_A$ 与 $cnt_B$ 呢？

我们记 $q=\displaystyle\bigg\lfloor\frac{x}{2^j}\bigg\rfloor$，$r=x\bmod 2^j$。

显然，如果 $q=0$，那么 $n$ 的最高位一定是 $2^{j-1}$。根据上面的式子，显然 $2^{j-1}$ 位置对答案的贡献为 $0$，因此我们只需循环到最大的 $j$ 使得 $2^j\le n$ 即可。

先记一个小结论：

$[1,2^j-1]$ 中有且只有 $[2^{j-1},2^j-1]$ 的 $2^{j-1}$ 位置为 $1$。

有了上面的限制，我们计算出的 $q$ 一定是正数，且显然有 $cnt_B=2^{j-1}$（理由：$2^j\le n$ 和上面的小结论）。我们只需考虑如何计算 $cnt_A$ 即可。

$cnt_A$ 分布在两部分中：被 $2^j$ 整除的部分（由 $q$ 代表）和整除完剩余的部分（由 $q$ 代表）。

• 对于每个整除产生的 $2^j$ 大小的块，根据上面的小结论，每个块对 $cnt_A$ 有恰好 $2^{j-1}$ 的贡献，因此这部分的总贡献就是 $q\times 2^{j-1}$；
• 对于剩余部分，还是根据上面的小结论，只有 $\ge 2^{j-1}$ 的部分会对 $cnt_A$ 有贡献，因此这部分的总贡献就是 $\max(0,r-2^{j-1}+1)$。

所以 $cnt_A=q\times 2^{j-1}+\max(0,r-2^{j-1}+1)$。

也就是说，第 $2^{j-1}$ 位对答案产生的贡献为 $\Big((q-1)\times 2^{j-1}+\max(0,r-2^{j-1}+1)\Big)\times 2^{j-1}$。

整合一下：(完全展开形式）

$$Ans=\displaystyle\sum_{j\gt 0,2^j\le n}\Bigg(2^{j-1}\times\bigg(\Big(\big\lfloor\frac{n}{2^j}\big\rfloor-1\Big)\times 2^{j-1}+\max\Big(0,(n\bmod 2^j)-2^{j-1}+1\Big)\bigg)\Bigg)$$

显然每一位的贡献可以时间复杂度 $\mathcal{O}(1)$ 完成，于是我们成功地把最终的时间复杂度降到了 $\mathcal{O}(\log n)$。

AC Code

按最终的式子计算就可以了，所以不展示。

乘法一定一定开 long long！！！ 不长记性

后记

感谢您的阅读！若有不妥之处还请批评指正！

题目传送门

题目描述

数轴上有 $n$ 个定点，其中点 $1$ 位于原点，点 $i(i\ge 2)$ 位于数轴上表示数 $x_i$ 的位置（$x_i\lt x_{i+1}$）。

这条数轴上还有 $m$ 条线段，第 $i$ 条线段的中点位于数轴上表示数 $z_i$ 的位置（$z_i$ 单调递增），从中点到线段两端点的距离都为 $l$（本题中，所有线段的 $l$ 都相同）。

对 $m$ 条线段进行 $d$ 次操作，第 $i$ 次操作将中点位于 $p_i$ 的一条线段移动至数轴上另一处，使得移动后线段的中点位置为 $r_i$（$p_i\neq r_i$）。保证移动前存在符合要求的线段，且移动后不会有其他线段的中点与该线段重合。

对于 $i=1,2,...,d$，输出执行第 $i$ 次操作之前，$n$ 个定点中被至少一条线段覆盖的点的数量（位于端点也算）。你还需要输出所有操作都完成后，$n$ 个定点中被至少一条线段覆盖的点的数量。

数据范围：$2\le n,m\le 5\times 10^5$，$1\le d\le 5\times 10^5$，$1\le l\le 10^9$，$0\lt x_i\le 10^9$，$0\le z_i,p_i,r_i\le 10^9$。

分析

注意到，题面中的操作很像扫描线中的“求线段长度并”的操作。那我们不妨就用扫描线的思想解决这道题。

显然，存在题目给定的数轴这一维和时间这一维。时间这一维由于题目的条件不用多加处理，因此我们只需处理数轴这一维。

开一棵线段树，区间对应题目中的定点区间。每次增加或删除一条线段就等价于增加或减少一次区间覆盖。

区间覆盖对应的线段树上操作是：如果当前节点表示的区间被修改区间完全包含，就直接执行覆盖/去覆盖的指令。否则向下递归，然后 Push_up。具体操作为：

• 每个节点维护该节点被完整覆盖的次数 $k$（初始为 $0$）和被覆盖的位置的个数 $sum$（初始也为 $0$），覆盖时把 $k$ 加上 $1$，去覆盖时把 $k$ 减去 $1$。
• 修改后，如果 $k=0$，叶子结点的 $sum$ 修改为 $0$，其他节点的 $sum$ 修改为两子节点的 $sum$ 之和；如果 $k\gt 0$，各节点的 $sum$ 修改为节点所对应的区间长度。(如果不注意加粗部分那么恭喜你数组越界了）

一个节点的 Push_up 的操作与修改后的操作一致。

初始时，二分（或使用 lower_bound 和 upper_bound 找出）线段左右端点的位置，如果存在受影响的位置（端点未越界且区间存在/右端点在左端点右边），那么就将对应的连续区间进行覆盖就可以了。

执行操作时，先删除线段，再添加线段，操作细节同初始时的操作。不要忘记输出初始时和结束时的答案哦！

建立线段树的时间复杂度是 $\mathcal{O}(n)$，初始覆盖及所有操作的总时间复杂度为 $\mathcal{O}((m+d)\log n)$，对于 4s 的时间限制还是绰绰有余的。

参考代码

#include <bits/stdc++.h>
using namespace std;
#define LL long long

#define N 500007

int n,x[N];//由于 Seg 函数，需要把 n 定义在全局

struct qwq{int l,r,k,sum;}t[N<<2];//线段树
#define L(u) u<<1
#define R(u) u<<1|1

inline void build(int u,int l,int r){//建树
    t[u]={l,r,0,0};
    if(l<r){
        int mid=(l+r)>>1;
        build(L(u),l,mid),build(R(u),mid+1,r);
    }
}

inline void Push_U(int u){//更新 sum
    if(t[u].k) t[u].sum=t[u].r-t[u].l+1;//被完整覆盖过
    else t[u].sum=t[L(u)].sum+t[R(u)].sum;//没被完整覆盖过
}

inline void Modify(int u,int l,int r,int val){
    if(l<=t[u].l&&t[u].r<=r){//完全包含
        t[u].k+=val;
        if(t[u].l==t[u].r) t[u].sum=min(t[u].k,1)*(t[u].r-t[u].l+1);//注意对叶子的特判（WA+RE*2）
        else Push_U(u);
        return;
    }
    int mid=(t[u].l+t[u].r)>>1;
    if(l<=mid) Modify(L(u),l,r,val);
    if(r>mid) Modify(R(u),l,r,val);
    Push_U(u);//更新当前节点
}

int l;//由于 Seg 函数，需要把 l 定义在全局，但线段树相关操作中存在以 l 命名的变量，故定义在此处

inline void Seg(int pos,int val){//线段覆盖/去覆盖
    int pl=lower_bound(x+1,x+n+1,pos-l)-x;//对应的区间左端点
    int pr=upper_bound(x+1,x+n+1,pos+l)-x-1;//对应的区间右端点
    if(pl<=pr) Modify(1,pl,pr,val);//如果区间合法，那么修改
}//左右端点别写反！！！

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);

    int m,d;
    cin>>n>>m>>d>>l;
    for(int i=2;i<=n;i++) cin>>x[i];
    build(1,1,n);//别忘了建树！！
    while(m--){
        int z;
        cin>>z;
        Seg(z,1);
    }
    cout<<t[1].sum<<'\n';//初始答案
    while(d--){
        int p,r;
        cin>>p>>r;
        Seg(p,-1),Seg(r,1);//先删后加
        cout<<t[1].sum<<'\n';//操作后答案
    }

    return 0;
}

感谢您的阅读！

题目传送门

题目描述

给定一个长为 $n$ 的自然数数列 $a$ 和一个正整数 $k$，问最少修改 $a$ 中的多少个整数（修改后必须也为整数）能使整个序列的所有长为 $k$ 的区间的元素和都为偶数。

数据范围：$1\le k\le n\le 10^6$，$0\le a_i\le 10^9$。

分析

首先，因为我们只关心结果的奇偶，所以我们可以直接将数列转为 $0/1$ 序列（所有数对 $2$ 取模），并将求和改为求异或和。

然后，我们注意到，这个数列中 $[i,i+k-1]$ 这个区间内元素的异或和与 $[i+1,i+k]$ 这个区间内元素的异或和相等（都为 $0$）。将两式异或，得到 $a_i\oplus a_{i+k}=0$，即 $a_i=a_{i+k}$。所以我们得到一个重要结论：修改后的序列中，下标模 $k$ 相等的位置上的数，奇偶性一定相同。

因此，我们可以计算序列中下标模 $k$ 相等的数中有多少个 $0$（偶数）和多少个 $1$（奇数）。设下标取模后的结果为 $r$（我的代码中 $r$ 取 $1$ 到 $k$），则 $cnt_{r,0}$ 表示这些数中偶数的个数，$cnt_{r,1}$ 类似（奇数的个数）。

这样，我们就将问题转化为了下面这样：

有一个长为 $k$ 的数列，第 $i$ 个位置上填 $0$ 会有 $cnt_{i,\color{red}1}$ 的代价，填 $1$ 会有 $cnt_{i,\color{red}0}$ 的代价（注意下标，是要改成目标数的数的个数，而非目标数的个数），且只能填 $0$ 或 $1$ 中的一个，不能不填。要求所有位上的数的异或和为 $0$，求最小总代价。

显然，我们可以 DP 解决。

设 $dp_{i,0}$ 表示第 $i$ 位填 $0$ 在以 $i$ 结尾的前缀中的最小总代价（$dp_{i,1}$ 类似，表示第 $i$ 位填 $1$），则根据异或运算的定义，我们可以很容易地得出：

$$dp_{i,0}=\max(dp_{i-1,0}+cnt_{i,1},dp_{i-1,1}+cnt_{i,0})$$

$$dp_{i,1}=\max(dp_{i-1,1}+cnt_{i,1},dp_{i-1,0}+cnt_{i,0})$$

特别地，当 $i=1$ 时，$dp_{1,0}=cnt_{1,1}$，$dp_{1,1}=cnt_{1,0}$。（如果你忘记了这条然后交了一发，你就会被 Test #1 给 hack 掉）

最后我们输出 $dp_{k,0}$ 就结束了。（如果下标采用 $0$ 到 $k-1$，请注意你的 DP 起终点和输出内容）

输入+处理 $cnt$ 数组的时间复杂度为 $\mathcal{O}(n)$，DP 的复杂度也为 $\mathcal{O}(n)$，所以完全没有问题！

代码的具体实现在上文中讲得很清楚，因此不展示。

感谢您的阅读！

题目传送门

题意简述

你有 $n$ 项工作要做，第 $i$ 项工作需要连续的 $d_i$ 天去完成（同一天只能完成一项工作），而且最后一天不得晚于 $t_i$。问在开始所有工作之前，你最多能休息多久？

数据范围：$1\le n\le 10^6$，$1\le d_i,t_i\le 10^9$。保证所有任务都能够按时完成。

解析

简单的贪心。

秉承“能拖就拖”的原则，我们先按截止时间降序排列这些任务，然后从前往后扫，同时维护一个值 $Ans$（根据数据范围，该值初始值应不小于 $10^9$）。

对于每个 $i$，执行下面这个式子：

$$Ans\leftarrow\min(Ans,t_i)-d_i$$

为什么？

首先第 $i$ 项工作需要在第 $t_i$ 天及之前完成，所以开始时间肯定不晚于 $t_i-d_i+1$。

如果即便拖延到极致但有工作已经占了第 $t_i$ 天，那么只能再往前推，推到最后一个没有工作的日子为止（第 $Ans$ 天）。

最后直接输出 $Ans$ 就可以了。

快排时间复杂度 $\mathcal{O}(n\log n)$，扫任务时间复杂度 $\mathcal{O}(n)$，可以通过本题。

代码实现过程已在上文中完整给出，因此不展示。

感谢您的阅读！

题目传送门

题意简述

给定一棵 $n$ 个节点的，以 $1$ 为根的有根树，请按升序输出所有满足下面要求的正整数 $k$：

• 这棵树可以被划分为 $k$ 个节点数目相同的连通块。

数据范围：$2\le n\le 3\times 10^6$。

解析

首先，我们需要找出可能成为连通块节点数目的所有正整数，记为 $d$。

显然，$d$ 必须是 $n$ 的因数。

如果将这部分的复杂度压缩至根号，不要忘记将数组排好序！！ 我不会告诉你我为什么要提醒这一条

然后，降序枚举 $d$（对于 $1$ 和 $n$ 我们可以不经判断直接输出），判断树可否分为若干大小都为 $d$ 的连通块。

方法使用贪心，具体实现如下：

• 对整棵树进行 DFS，同时维护布尔值 $Ans$（初始为 $1$）。对每个节点记录在其子树中且与该节点位于同一连通块的节点数，保存为 $sz$ 数组。为表述方便，记每个连通块的大小为 $sz_0$（与当次的 $d$ 相等）。
• 搜索到节点 $u$ 时，如果 $Ans=0$ 那么将 $sz_u$ 归零后返回（避免无用初始化）。
• 如果 $Ans=1$，搜索 $u$ 的每个子节点 $v$。
• 返回时：

  • 如果 $sz_u\gt sz_0$，那么将 $Ans$ 设为 $0$ 并返回；
  • 如果 $sz_u=sz_0$，那么直接返回；
  • 如果 $sz_u\lt sz_0$，那么将 $sz_{fa_u}$ 加上 $sz_u$ 并返回（$fa_u$ 为 $u$ 的父亲）。
  • 无论哪种情况，返回前必须将 $sz_u$ 设为 $0$。

• 整棵树搜完后，判断 $Ans$ 是否仍然为 $1$。若是，则 $\frac{n}{sz_0}$ 为答案。

接下来证明这种方法的正确性。

假设这是我们第一次割下来的，大小为 $sz_0$ 的块。如果我们不割它，那么显然没有别的解法。所以，有块，一定割。

再假设在一棵子树中能割的块都割完了，但剩下的大小大于 $sz_0$。显然，如果各个子节点还能割的话一定就割了，所以现在各个子节点的 $sz$ 值均小于 $sz_0$。我们不能抛下任意一棵子树（否则大小就不等于 $sz_0$ 了），所以此时一定无解。那么对于大小小于 $sz_0$ 的 $sz$ 值，我们只能选择把这个节点的剩余连通部分交给父节点去割。

所以每次验证 $d$ 是否可行都需要一次 $\mathcal{O}(n)$ 的 DFS。那么 $n$ 的正整数因数个数到底有多少呢？

这个答案有个相当宽松的上界，$2\sqrt{n}$。但在 $n\le 3\times 10^6$ 的条件下，较大的 $n$ 显然不可能达到这个值。事实上，题目范围内含有最多正整数因子的数为 $2\ 882\ 880$，含有 $336$ 个因子。而题目的时间限制是 10 秒，所以我们的算法肯定可以通过！（亲测，当 $n=10^3$ 时，$\mathcal{O}(n^3)$ 的区间 DP 关同步流甚至跑不到 500ms）

参考代码

#include <bits/stdc++.h>
using namespace std;
#define LL long long

#define _ 507
int d[_];//存n的因子

#define N 3000007

int cnt,head[N];
struct qwq{int v,nxt;}edge[N];//链式前向星存边
inline void AddE(int u,int v){
    edge[++cnt]={v,head[u]};
    head[u]=cnt;
}

bool Ans;//是否有解
int sz[N];//剩余块大小

inline void dfs(int u,int fa,int sz0){
    sz[u]++;//自己也得算
    for(int i=head[u];i;i=edge[i].nxt){
        int v=edge[i].v;
        dfs(v,u,sz0);
        if(!Ans) {sz[u]=0;return;}//记得归零
    }
    if(sz[u]>sz0) {sz[u]=0;Ans=0;return;}//记得归零
    if(sz[u]==sz0) {sz[u]=0;return;}//记得归零
    sz[fa]+=sz[u];sz[u]=0;//记得归零
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);

    int n,m=0;
    cin>>n;
    for(int i=2;i*i<=n;i++)//根号判因数
        if(n%i==0){
            d[++m]=i;
            if(i*i!=n) d[++m]=n/i;
        }
    sort(d+1,d+m+1);//如果根号判因数一定要记得sort！！
    for(int i=2,a;i<=n;i++) cin>>a,AddE(a,i);//父节点到子节点

    cout<<1<<' ';//显然
    for(int i=m;i;i--){
        sz[0]=0,Ans=1;dfs(1,0,d[i]);//d为连通块大小
        if(Ans) cout<<n/d[i]<<' ';//输出的为连通块个数
    }
    cout<<n<<'\n';//显然

    return 0;
}

感谢您的阅读！

题目传送门

题意简述

给定一个整数 $n$（$2\le n\le 10^{14}$），在 $n\gt 1$ 时重复执行：

• 如果 $n$ 是偶数，那么让 $n$ 变为原来的一半（$n\leftarrow\frac{n}{2}$）；
• 如果 $n$ 是奇数，那么让 $n$ 变为 $3\times n+3$（$n\leftarrow 3n+3$）。

问是否能在有限次步数内结束操作。是输出 TAK，否输出 NIE。

分析

结论题。

没有思路，不妨画个图表示一下变换的过程（请读者自行画图）。画了一段时间后不难发现，能走到点 $1$ 的点只有 $2,4,8,...$ 这些编号为 $2^k$ 的点。猜测当且仅当 $n$ 是 $2$ 的正整数次幂时，操作能在有限步数内结束。

下面来证明一下这个结论。充分性是显然的，接下来证必要性。

如果 $n$ 不是 $2$ 的正整数次幂，由于 $n\ge 2$ 且 $n$ 为正整数，故 $n$ 的质因数分解中必存在奇数因子。

操作时，根据规则，$n$ 中 $2$ 的幂次将降至 $0$，然后执行 $n$ 为奇数时的操作。

等等！$3n+3=3(n+1)$，也就是说 $n$ 在执行完这次操作之后一定会带上 $3$ 这个因子！

此后 $n$ 为偶数的操作中，$3$ 这个因子无法被消除，到 $n$ 重新变为奇数之前，$3$ 这个因子永远会存在。再次进行了 $n\leftarrow 3(n+1)$ 这个操作后，$3$ 这个因子仍然是存在的！

因此，我们得出结论：只要 $n$ 不是 $2$ 的倍数，那么它将会永远被 $3$ 所支配（操作不会结束）！！

必要性得证，因此问题转化为了判断 $n$ 是不是 $2$ 的幂次。方法很多，我的方法是转化为判断 $n=\text{lowbit}(n)$ 是否成立（怎么算 $\text{lowbit}$ 请参考你的树状数组，或者你可以枚举 $2$ 的幂次），时间复杂度 $\mathcal{O}(1)$（当然 $\mathcal{O}(\log n)$ 的做法也能接受）。

代码难度很低，请自行完成。

尾声

感谢您的阅读，若有不妥还请批评指正。

题目传送门

题意简述

给定两个正整数 $n$ 和 $k$（$2\le n\le 10^6$，$1\le k\le n$），请输出一个长为 $n$ 的排列，使得其中相邻两项的差的绝对值都不小于 $k$。如果无解，请输出 NIE。

解析

构造题。

我们建一张 $n$ 个节点的无向图，图中两个点有连边当且仅当它们在排列中可以挨着。

我们看看每个节点与编号比自己小的节点的连边情况。

• 对于 $1\le u\le k$ 的节点 $u$，没有编号比 $u$ 小的节点与 $u$ 连边。
• 对于 $k+1\le u\le n$ 的节点 $u$，编号在 $[1,u-k]$ 内的所有节点都与 $u$ 有连边。

根据题意，我们需要找出这张图中的一条哈密顿路径（通过每个节点恰好一次的通路）。

首先，哈密顿路径存在的一个必要条件是图连通。显然，对于点 $k$ 被孤立的情况（$n-k\lt k$，即 $n\lt 2k$）一定是无解的。

然后，如果 $n=2k$，那么 $k$ 只与 $n$ 有连边，也就是说路径的一个端点必须为 $k$。容易发现，$[k,n,k-1,n-1,...,1,k+1]$ 是一条合法路径。

如果 $n\gt 2k$，按 $n$ 的奇偶性分类讨论：

• 如果 $n$ 是奇数，那么我们可以先输出 $\frac{n+1}{2}$（$1$ 到 $n$ 的中点），然后按照 $n,\frac{n+1}{2}-1,...,\frac{n+1}{2}+1,1$ 的顺序输出即可。

正确性证明：$n-\frac{n+1}{2}=\frac{n-1}{2}$，由于 $n,k$ 都是整数，所以 $\frac{n-1}{2}\ge\frac{2k}{2}=k$。

• 如果 $n$ 是偶数，那么 $[n,\frac{n}{2},...,\frac{n}{2}+1,1]$ 是一个合法路径。

正确性证明：$n-\frac{n}{2}=\frac{n}{2}\gt\frac{2k}{2}=k$。

所以，我们并不需要真的建一张图，只需要判一下 $n$ 与 $2k$ 的大小关系然后按情况输出就可以了。时间复杂度 $\mathcal{O}(n)$。

代码难度极低，因此参考代码不予展示。

尾声

感谢您的阅读，若有不妥还请批评指正。

题目传送门

题面过于抽象，受笔者语文水平所限，就不在此翻译了，烦请各位读者自行理解。

探索

这是笔者第一道自己做的构造题。

我们不妨采用如下的顺序接吻：（用 C++ 语言表示）

void kiss(int Boy,int Girl){}

for(int i=1;i<=n;i++)
    for(int j=1;j<=n;j++)
        kiss(i,j);

其中 $Boy$ 表示男生编号，$Girl$ 表示女生编号。下面分别简称编号为 $i$ 的男生和女生为“男 $i$”和“女 $i$”。

笔者首先依次思考了 $n=3$ 和 $n=4$ 的情况，很快就想了出来。但是发现相同的方法对 $n=5$ 和 $n=6$ 的情况不适用（总是少一张纸）。因此，我重新思考了 $n=5$ 时的构造方案：

在开始安排之前，算一算，有 $\lfloor\frac{3\times 5}{2}\rfloor=7$ 张纸可以用。然后，思考亲吻的具体流程。

首先还是男 $1$ 亲遍所有女生。显然在男 $1$ 亲遍前 $(n-1)$ 个女生之前，男 $1$ 亲的那张纸的反面是不能动的。所以前 $(n-1)$ 个女生总是隔着（每次都不同）的一张纸巾和男 $1$ 接吻。如下：（蓝笔写的编号代表男生，红笔写的编号代表女生，黑笔写的编号为纸巾编号，灰线连接的两个面为接触面）

最初尝试的时候发现如果女 $n$ 直接和男 $1$ 用同一张纸亲会出问题，所以这次我们让女 $n$ 和前面 $(n-1)$ 名女生一样，也隔着一张纸巾和男 $1$ 接吻：

轮到男 $2$ 了。发现如果男 $2$ 如果直接用男 $1$ 用过的那张纸反面去亲遍女生会出大问题，让男 $2$ 新拿一张纸的话……没想过。（AC 掉这道题之后发现可以实现，只不过是顺序上的差异）所以，干脆大胆一点，直接让男 $2$ 和各位女生都只用一张纸巾亲吻！（这么说可能会引起误会，以下图所描述的情况为准）便宜男 $2$ 了

轮到男 $3$。发现男 $3$ 如果用男 $1$ 用过的那张纸反面的话会出大问题，所以要让男 $3$ 拿一张没用过的纸巾。但是……（本题解最关键的部分来了）男 $3$ 的亲法很有讲究。先用他亲的这张纸反面接触男 $1$ 亲过的那张纸反面（都是空白），然后让男 $1$ 亲过的那面与男 $2$ 亲过的那面接触，男 $2$ 亲过的那面的反面就是女生们亲的面了。

感觉没看懂？看下面这张图就明白了：

太乱了？看看这个局部图：

图中紫色的两个（空白）面相互接触，蓝灰色的两个面相互接触。这样，男 $3$ 和女生之间，就隔了 $3$ 张纸。

轮到男 $4$。男 $4$ 肯定不能拿男 $3$ 亲过的那张纸的反面去亲（男 $3$ 的细菌蹭到别的空白面上，浪费了），但是……他可以拿男 $1$ 亲过的那张纸的反面去亲！如下图：

最后是男 $5$。这次，男 $5$ 终于可以用男 $3$ 用过的那张纸的反面去亲女生了！

整体的纸巾使用情况如图：

正好一面不落，全都用过了！

对于 $n=6$ 的情况。我们发现，可以“浪费”掉男 $1$ 亲过的那张纸的反面，最终情况如下图：

按照这个思路，我们很快就能构造出 $n=7,8,9,...$ 的方案。

感觉正解已经出来了，那么总结一下规律吧。

规律及正确性证明

不妨设 $m=\lfloor\frac{3n}{2}\rfloor$，即纸的总张数。

则整个方案如下图所示（注意顺序）：

（第五步中，编号 $1$ 的纸巾的两个面标反了；这一步实际上可以通过省去 $1$ 号纸巾简化为两张纸，下文中提到的我的提交记录中使用的就是两张纸的亲法）

我们来证明一下这个方案的正确性。

除了男 $2$ 外，其余男生用的编号最大的纸巾的编号为

$$\bigg\lfloor\frac{n-2}{2}\bigg\rfloor+1$$

它等于

$$\bigg\lfloor\frac{n}{2}-1\bigg\rfloor+1$$

也就是

$$\bigg\lfloor\frac{n}{2}\bigg\rfloor-1+1$$

最后两项抵消，得

$$\bigg\lfloor\frac{n}{2}\bigg\rfloor$$

女生和男 $2$ 一共用过 $n$ 张纸，我们发现

$$\bigg\lfloor\frac{n}{2}\bigg\rfloor+n=\bigg\lfloor\frac{n}{2}\bigg\rfloor+\frac{2n}{2}=\bigg\lfloor\frac{3n}{2}\bigg\rfloor$$

一张不多，一张不少！

再来看看一共输出了多少个数。

满打满算，因为在我们的方案中，每对男女接吻至多需要用三张纸，所以我们大胆一点，不妨假设每对男女都用了三张纸。

一共 $n^2$ 对男女，每对所需输出的数的个数为 $2+1+2\times 3=9$，一共需要 $9\times 1000^2=9\times 10^6$ 张纸，远小于题目要求的 $5\times 10^7$，所以是完全合法的！

AC 代码

总结了规律后，我们就有了这个提交记录中的那份代码（完全可以把 $n=2$ 的特判给删掉，因为算出来的 $p=q=0$；$n=1$ 的特判不能删，删了还得加其他特判）。代码仅供参考，方案中存在可以改动的地方，所以请不要抄袭代码。

再次提醒，代码中第五步的操作只用了两张纸，与上文图中所示方法有所不同（省去了 $1$ 号纸巾）。

建议使用较快的输出，毕竟输出量还是挺大的。

尾声

感谢您的阅读，若有不妥之处还请批评指正。

#219. PIN

时间限制：200ms

空间限制：256MB

题意简述

给定正整数 $n$，求满足以下所有条件的整数三元组 $(a,b,c)$ 的数量：

• $0\lt a\lt b\lt c$；
• $a+b+c=n$；
• 设 $b=k_1a$，$c=k_2a=k_3b$，则 $k_1,k_2,k_3$ 均为整数。

输入格式

一行一个正整数 $n$（$1\le n\le 10^9$）。

输出格式

一行一个整数，表示满足条件的三元组数量。

输入输出样例

样例输入

35

样例输出

2

说明/提示

样例解释

两个三元组分别为 $(1,2,32)$ 和 $(5,10,20)$。

探索

显然 $k_2=k_3\times k_1$。

所以 $b=k_1a$，$c=(k_1\times k_3)a$。

进一步得 $n=(1+k_1+k_1\times k_3)a$。

由于 $a\lt b\lt c$，所以 $k_1,k_3\ge 2$。

设 $k=k_1\times k_3+k_1+1$，则 $k\ge 7$。

同时，$k-1=k_1\times k_3+k_1=k_1\times(k_3+1)$，故 $k-1$ 也要能够被表示为一个不小于 $2$ 的正整数和一个不小于 $3$ 的正整数的积才行。

所以，当 $k$ 确定时，满足条件的二元组 $(k_1,k_3)$ 个数即为 $k-1$ 的因数个数减二（不是 $1\times (k-1)$）再减一（如果 $(k-1)$ 是偶数那么 $k_3+1\ge 3$）。

再来看一下样例。

$n=35=35\times 1=7\times 5$。由于这两组反过来都会有 $k\lt 7$，所以只有这两种拆分方案。

$35-1=34=2\times 17$，$7-1=6=2\times 3$，两个数都具有唯一拆法，所以答案为 $2$。

考虑首先把 $n$ 的所有因子找出来，找完后暴力枚举所有大于等于 $7$ 的因子，将他们减一后算出各自的合法拆分数就可以了。

至于时间复杂度？一个数的因子少之又少，所以根本不需要花什么时间。实际上，不考虑排序，复杂度大概为 $\sqrt{n}$ 乘上一个常数（量级与 $n$ 的因子个数相同）。相信自己，勇敢尝试，不断进步，让我们体验成功带来的自信，从而走向自强吧！

AC 代码

#include <bits/stdc++.h>
using namespace std;
#define LL long long

#define N 100007
int cnt,a[N];

inline bool check(int v,int k){//对于k3的判定
    return v!=1&&v!=k&&v!=2;
}

inline int Count(int k){//计算 k-1 的合法拆分方案数
    int res=0;
    for(int i=1;i*1ll*i<=k;i++)
        if(!(k%i)){
            res+=check(i,k);
            if(i*i!=k) res+=check(k/i,k);//注意平方数的判断（比如说9）
        }
    return res;
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);

    int n,ans=0;
    cin>>n;
    if(n<7){cout<<0<<'\n';return 0;}//特判：无方案
    for(int i=1;i*1ll*i<=n;i++)//根号复杂度筛因子
        if(!(n%i)){
            a[++cnt]=i;
            if(i*i!=n) a[++cnt]=n/i;
        }
    sort(a+1,a+cnt+1);//将所有因子从小到大排序
    for(int i=cnt;i&&a[i]>=7;i--)
        ans+=Count(a[i]-1);//检查每个因子是否能作为 k
    cout<<ans<<'\n';

    return 0;
}

纯纯乐子题的乐子题解，看着玩就好。如果有什么不妥之处还请批评指正。

题目传送门

题目描述

给定一张含有 $N$ 个节点的 有向无环图（题中没有明说，但是由于没有不合法情况，故可以知道），节点编号从 $1$ 到 $N$。只有编号在 $1$ 到 $L$ 之间的 $L$ 个节点出度不为 $0$。保证编号在 $L+1$ 到 $N$ 之间的 $N-L$ 个节点入度均不为 $0$。

现在，将点 $1$ 的点权设为 $1$，并重复执行以下操作，直至编号在 $1$ 到 $L$ 中的所有节点点权均为 $0$ 为止：

• 选出点 $x$，满足 $1\le x\le L$，且点 $x$ 的点权大于 $0$。
• 对于每一条从 $x$ 出发的有向边，将到达的节点的点权加上 $x$ 的点权。
• 将点 $x$ 的点权设为 $0$。

在所有操作结束后，回答下面两个问题：

• 编号在 $L+1$ 到 $N$ 之间的所有点的点权和是多少？由于结果可能很大，输出其对 $10^9+7$ 取模的结果；
• 编号在 $L+1$ 到 $N$ 之间的所有点中，点权不为 $0$ 的点的个数是多少？

解析

很简单的一道题。

考虑拓扑排序，这样可以将同一节点上的所有操作一次性处理完。

记 $dp_i$ 为点 $i$ 的点权（对于编号在 $1$ 到 $L$ 之间的所有节点，其点权为操作期间所有下放到该点的点权之和），$vis_i$ 表示点 $i$ 由点 $1$ 出发是否可达。初始时 $dp_i$ 为 $1$，$vis_i$ 为 true。

显然，$dp_i$ 为所有有边连向点 $i$ 的点的 $dp$ 值之和，$vis_i$ 为所有有边连向点 $i$ 的点的 $vis$ 值的逻辑或。

然后就是一道简单的拓扑排序+递推了。时间复杂度 $\mathcal{O}(N+\sum K)$。

代码参见这个提交记录，请勿抄袭！

别把 e[x].size() 写成 e[i].size() 啊

谢谢阅读，点个赞吧~