跛脚国王在一个大小为 $n \times m$ 的棋盘上移动，每一步都从当前格子移动到一个共边的相邻格子。我们用 $(x, y)$ 表示位于第 $x$ 行、第 $y$ 列的格子。

跛脚国王需要遍历棋盘上的所有格子，并且每个格子恰好访问一次，最后回到起始格子。此外，在棋盘上指定了两个相邻的格子 $(x_1, y_1)$ 和 $(x_2, y_2)$。在国王的遍历路径中，这两个格子必须相邻出现：也就是说，一旦国王到达其中一个格子，就必须立刻移动到另一个格子。

请输出一种符合条件的遍历顺序，或者判断这样的遍历是否不存在。

输入格式

第一行包含两个整数 $n$ 和 $m$（$2 \le n, m \le 1000$）——棋盘的尺寸。

第二行包含四个整数 $x_1, y_1, x_2, y_2$——两个相邻格子的坐标（$1 \le x_1, x_2 \le n$；$1 \le y_1, y_2 \le m$；$|x_1 - x_2| + |y_1 - y_2| = 1$）。

输出格式

如果不存在这样的遍历，请输出一个整数 $-1$。

否则，请输出 $n \times m + 1$ 对整数——按照遍历顺序给出的格子坐标。起始格子需要输出两次：一次在开头，一次在结尾。

子任务

本题共有 50 个测试点，每个测试点独立计分，价值 2 分。

在比赛过程中，你可以看到每个测试点的判题结果。

样例数据

标准输入

4 3
2 2 3 2

标准输出

1 1
2 1
2 2
3 2
3 1
4 1
4 2
4 3
3 3
2 3
1 3
1 2
1 1

标准输入

3 5
1 2 2 2

标准输出

-1

说明

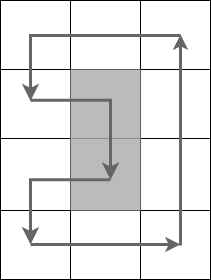
图中展示了第一个样例的一种棋盘遍历方式。