The lame king moves on a grid board of size $n \times m$, each time moving from the current cell to a side-adjacent neighboring cell. We denote the cell in row $x$ and column $y$ as $(x, y)$.
The lame king must visit all cells, visiting each cell exactly once, and return to the starting cell. At the same time, two neighboring cells $(x_1, y_1)$ and $(x_2, y_2)$ are marked on the board. In the king’s traversal of the board, the cells $(x_1, y_1)$ and $(x_2, y_2)$ must appear consecutively: after being in one of them, he must immediately move to the other.
Output a suitable order of traversal of the board, or determine that it does not exist.
Input Format
The first line contains two integers $n$ and $m$ $(2 \le n, m \le 1000)$ — the board dimensions.
The second line contains four integers $x_1, y_1, x_2, y_2$ — the coordinates of two neighboring cells $(1 \le x_1, x_2 \le n;\ 1 \le y_1, y_2 \le m;\ |x_1 - x_2| + |y_1 - y_2| = 1)$.
Output Format
If such a traversal does not exist, output a single number $-1$.
Otherwise, output $n \times m + 1$ pairs of numbers — the coordinates of the cells in the order of traversal; the starting cell must be printed twice, at the beginning and at the end.
Scoring
There are 50 tests in this problem, each scored independently with 2 points.
During the contest, you are informed of the checking result on each test.
Example
Standard Input
4 3 2 2 3 2
Standard Output
1 1 2 1 2 2 3 2 3 1 4 1 4 2 4 3 3 3 2 3 1 3 1 2 1 1
Standard Input
3 5 1 2 2 2
Standard Output
-1
Note
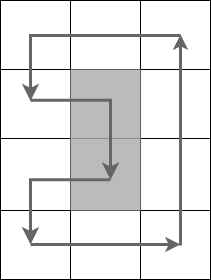
The figure shows a traversal of the board for the first example.