Siedmionogie pająki żyjące w Bajtocji budują pajęczyny o bardzo regularnej strukturze. Pajęczyna taka składa się z węzła centralnego, w którym zazwyczaj odpoczywa pająk, i $ d $ kręgów, ponumerowanych liczbami od 1 do $ d $. Każdy krąg to cykl złożony z węzłów połączonych nićmi.
Każdy węzeł, oprócz tych na kręgu $ d $, połączony jest nićmi z siedmioma innymi węzłami. Węzeł centralny jest połączony ze wszystkimi siedmioma węzłami z kręgu 1. Każdy węzeł z kręgu $ i $ jest połączony z $ k \in \{1, 2\}$ węzłami z kręgu $ i - 1$, dwoma sąsiednimi węzłami z kręgu $ i $ oraz $ l = 5 - k $ kolejnymi węzłami z kręgu $ i + 1$. Pierwszy i ostatni z tych $ l $ węzłów jest połączony z dwoma sąsiednimi węzłami z kręgu $ i $, a pozostałe tylko z jednym. Sieć można zawsze narysować na płaszczyźnie tak, by nici nie przecinały się. Sytuację pokazuje poniższy rysunek.
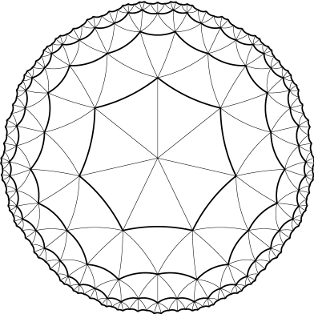
Sieci takie są bardzo skuteczne. Ostatnio Bajtazar zaobserwował spacer pająka po sieci o $ d $ = 10^{9} kręgach. Pająk zaczął w węźle centralnym, a następnie, poruszając się po niciach, wrócił do punktu wyjścia, nie przechodząc przez żaden węzeł więcej niż raz. W każdym węźle we wnętrzu wielokąta, po którego brzegu poruszał się pająk, została złowiona mucha. Bajtazar zanotował sobie kolejne ruchy pająka podczas spaceru i chciałby obliczyć, ile much zostało złapanych.
Input Format
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $ n $ ($3 \le n \le 7\,777\,777$) oznaczającą długość spaceru pająka, czyli liczbę odwiedzonych przez niego węzłów.
W drugim wierszu znajduje się ciąg $ n $ liczb całkowitych $ z_{i} $ ($1 \le z_{i} \le 6$). Opisuje on kolejne zakręty, jakie wykonywał pająk w trakcie spaceru. Z $ i $-tego węzła na ścieżce pająk wyszedł $ z_{i} $-tą nicią w kolejności zgodnej z kierunkiem ruchu wskazówek zegara, przy czym za nić 0 uznajemy nić, którą pająk wszedł do węzła. Wartość $ z_{1} $ dotyczy pierwszego węzła napotkanego po wyjściu z węzła centralnego, zaś $ z_{n} $ opisuje zakręt, jaki musiałby wykonać pająk w węźle centralnym, gdyby chciał przejść całą trasę raz jeszcze.
Output Format
Twój program powinien wypisać na wyjście jedną liczbę całkowitą - liczbę węzłów sieci wewnątrz wielokąta, który obszedł pająk.
Example
Input
10 2 2 2 2 3 2 2 2 2 3
Output
2
Notes
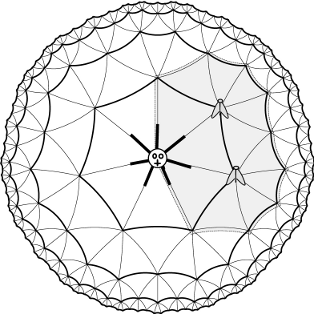
Wielokąt na rysunku oznacza trasę pająka. We wnętrzu wielokąta znajdują się dwa węzły. Zwróć uwagę, że nie liczymy węzłów na brzegu wielokąta.