七足蜘蛛生活在Bajtocja（拜托恰），它们会建造结构非常规整的蛛网。这样的蛛网由一个中央节点（通常蜘蛛就在这里休息）和 $d$ 个环组成，这些环按顺序编号为 1 到 $d$。每一个环都是由节点和丝线连接成的一个环形。

除了第 $d$ 个环上的节点以外，每个节点都通过丝线与其他七个节点相连。中央节点通过丝线与第 1 个环上的全部七个节点相连。第 $i$ 个环上的每个节点与第 $i-1$ 个环上的 $k \in {1,2}$ 个节点相连，并与本环上相邻的两个节点相连，还与第 $i+1$ 个环上连续的 $l=5-k$ 个节点相连。这 $l$ 个节点中的第一个和最后一个都与本环上的两个相邻节点相连，其余的只与一个相邻节点相连。这样的网络总是可以在平面上画出来，且不会出现丝线交叉。下图展示了这种情况。

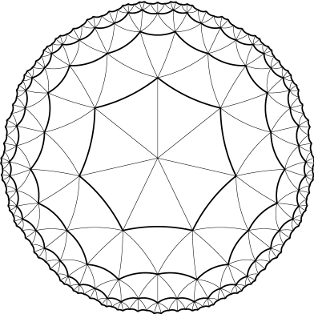
这种蛛网非常高效。最近，Bajtazar 观察到一只蜘蛛在有 $d = 10^9$ 个环的蛛网上散步。蜘蛛从中央节点出发，沿着丝线移动，最终回到起点，并且没有重复经过任何一个节点。在蜘蛛行走路径所围成的多边形内部的每一个节点上，都有一只苍蝇被捕获。Bajtazar 记录了蜘蛛散步时的每一步，并希望计算一共捕获了多少只苍蝇。

输入格式

输入的第一行包含一个整数 $n$ （$3 \le n \le 7,777,777$），表示蜘蛛散步的长度，也就是它经过的节点数。

第二行包含一个由 $n$ 个整数 $z_{i}$ （$1 \le z_{i} \le 6$）组成的序列，描述了蜘蛛在散步过程中每一步的转弯方式。蜘蛛在路径的第 $i$ 个节点，是沿顺时针方向的第 $z_{i}$ 根丝线离开该节点，其中编号为 0 的丝线是蜘蛛进入该节点时所经过的那根。$z_{1}$ 对应蜘蛛从中央节点出来后遇到的第一个节点的转弯方式，$z_{n}$ 则描述了如果蜘蛛要再走一遍完整路径时，在中央节点所需的转弯方式。

输出格式

你的程序应输出一个整数——蜘蛛所围成的多边形内部的网络节点数。

示例

输入

10
2 2 2 2 3 2 2 2 2 3

输出

2

说明

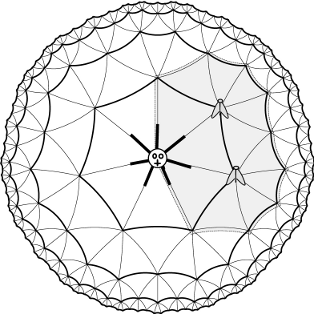
图中多边形表示蜘蛛的路线。多边形内部有两个节点。注意，处于多边形边界上的节点不计入结果。