Bajtokrąg składa się z $ n $ miast, ponumerowanych liczbami od 0 do $ n - 1$ i rozmieszczonych w specyficzny sposób. Dokładnie $ n-1 $ z nich leży na okręgu - są to kolejno miasta o numerach $1, 2, \ldots, n-1$. Pary kolejnych miast na okręgu połączone są dwukierunkowymi drogami. Stolica Bajtokręgu (miasto o numerze 0) leży w samym środku okręgu i jest połączona drogami ze wszystkimi innymi miastami.
Znamy czas przejazdu każdą drogą w Bajtokręgu. Władze Bajtokręgu chciałyby ułatwić mieszkańcom komunikację między miastami. W tym celu chcą wybrać dwa najbardziej oddalone miasta (w sensie czasu przejazdu między nimi) i wybudować w nich lotniska.
Input Format
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą $ n $ ($3 \le n \le 500\,000$), oznaczającą liczbę miast Bajtokręgu. Drugi wiersz zawiera $ n-1 $ liczb całkowitych dodatnich oznaczających czas przejazdu między kolejnymi miastami na okręgu (tzn. $ i $-ta liczba oznacza czas przejazdu między miastem o numerze $ i $ i następnym w kolejności miastem na okręgu). Trzeci wiersz zawiera $ n-1 $ liczb całkowitych dodatnich oznaczających czas przejazdu między stolicą a miastami na okręgu (tzn. $ i $-ta liczba oznacza czas przejazdu między stolicą a miastem o numerze $ i $). Zakładamy, że suma wszystkich czasów przejazdu między sąsiednimi miastami jest nie większa niż $10^{9}$.
Output Format
Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą - czas przejazdu między najbardziej odległą parą miast Bajtokręgu.
Example
Input
6 1 4 5 1 6 3 5 1 8 2
Output
7
Notes
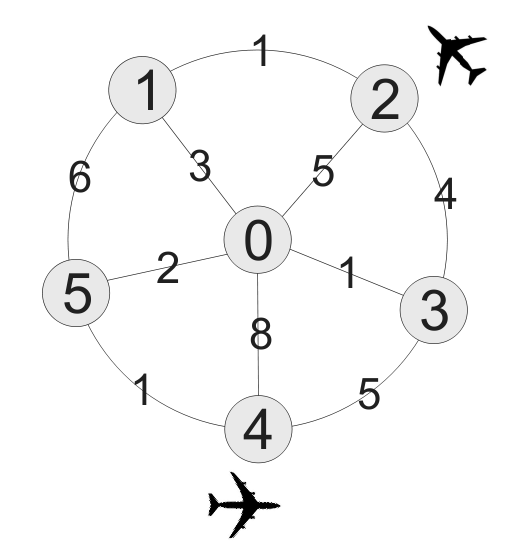
Para najbardziej oddalonych miast to (2, 4), a czas przejazdu między nimi wynosi 7. W tych właśnie miastach należy wybudować lotniska.