Bajtazar od dziecka marzył o działce w Puszczy Bajtockiej. Obecnie pracuje jako informatyk i wreszcie może sobie pozwolić na realizację tego marzenia.
Spółka Lasy Bajtockie właśnie rozpoczęła sprzedaż działek w nowym fragmencie puszczy, a Bajtazar zgłosił się jako pierwszy klient. Ów fragment puszczy z lotu ptaka wygląda jak kwadrat o wymiarach $ k \times k $ i rośnie w nim $ n $ sosen. Jako pierwszy klient Bajtazar ma do wyboru wiele ofert lokalizacji działki. Każda z ofert ma postać prostokąta położonego w całości we fragmencie puszczy. Bajtazar nie wie jeszcze, którą ofertę wybrać.
Po zakupie działki Bajtazar zamierza ogrodzić ją płotem. Bajtazar jest oszczędny i chciałby, żeby płot był jak najkrótszy, a zarazem ogradzał wszystkie drzewa rosnące na terenie działki. To, w szczególności, oznacza, że nie cały teren prostokątnej działki musi zostać ogrodzony. Bajtazar wie również, że każdego roku będzie musiał odprowadzić podatek gruntowy, którego wysokość będzie proporcjonalna do powierzchni ogrodzonego obszaru działki. I to głównie ten niemały podatek martwi Bajtazara.
Pomóż Bajtazarowi w podjęciu decyzji i oblicz, dla każdej zaproponowanej przez Lasy Bajtockie lokalizacji działki, jak duża byłaby powierzchnia ogrodzonego obszaru działki.
Input Format
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ k $ oraz $ n $ ($1 \le k \le 1\,000\,000$, $3 \le n \le 3\,000$), oznaczające długość boku fragmentu puszczy i liczbę sosen rosnących w tym fragmencie. Każdy z kolejnych $ n $ wierszy zawiera dwie liczby całkowite $ x_{i}, y_{i} $ ($0 \le x_{i} , y_{i} \le k $), oznaczające współrzędne punktu, w którym znajduje się $ i $-ta sosna. Możesz założyć, że w każdym punkcie znajduje się co najwyżej jedna sosna.
Kolejny wiersz wejścia zawiera jedną liczbę całkowitą $ m $ ($1 \le m \le 1\,000\,000$), oznaczającą liczbę możliwych lokalizacji działki. Każdy z kolejnych $ m $ wierszy zawiera cztery liczby całkowite $ a_{j}, b_{j}, c_{j}, d_{j} $ ($0 \le a_{j} \le b_{j} \le k $, $0 \le c_{j} < d_{j} \le k $), opisujące prostokątną działkę $[ a_{j}, b_{j} ] \times [ c_{j} , d_{j} ]$.
Output Format
Twój program powinien wypisać na wyjście $ m $ wierszy; $ j $-ty z tych wierszy powinien zawierać jedną liczbę rzeczywistą, podaną z dokładnością do jednej cyfry po kropce dziesiętnej: pole ogrodzonego obszaru działki przy wyborze $ j $-tej oferty. Możesz założyć, że pole to będzie zawsze dodatnie.
Example
Input
9 7 1 1 1 3 3 3 3 1 6 5 6 6 7 3 3 0 4 0 4 2 7 0 7 3 7 3 6
Output
4.0 10.0 6.0
Notes
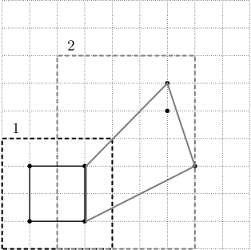
Rysunek przedstawia pierwsze dwie oferty lokalizacji działki z zaznaczeniem ogrodzonego obszaru.