Bytemon, a well known burglar, wants to rob the National Museum of Byteotia. He particularly is interested in the Royal Family Jewels, which are displayed in the most magnificent hall of the museum. There are $n$ exhibits watched over by $m$ guards in this hall. The museum's custodian wanted to ensure that the visitors, admiring exhibits, are not being disturbed by the guards more than necessary. Therefore, he ordered them to keep their set positions all the time, and look in one direction only.
Bytemon managed to get plan of this hall, where all the exhibits have been marked, as well as the arrangement of the guards. He obtained a quotation on all displayed jewels from a jeweller he knew. He also learned how much it would cost to discretely persuade each guard to close his eyes to Bytemon's activities at the time of the burglary.
Bytemon is wondering now how rich he can get. Therefore, he wants to chose the guards to be bribed, in such a way that the total value of the gems that are not in sight of any of guards that have not been bribed, less the cost of bribing selected guards, is as large as possible.
Input
The first line of input contains two integers $n$ and $m$ ($1 \leq n, m \leq 200\,000$), describing the number of exhibits and the number of guards. To describe their positioning assume that the museum plan has a rectangular coordinate system imposed. The second line of the input contains two integers $w$ and $h$ ($1 \leq w, h \leq 10^9$), describing the field of vision of the guards. Each of the guards is looking in the direction of decreasing y-coordinates, and the tangent of half of the angle of his view amounts to $w/h$. For simplicity, we assume that the guards and the exhibits are of a negligible size. The guard is observing all the exhibits, which are located in his field of vision (including the edge), even in case they are occluded by other exhibits or guards.
Subsequent $n$ lines describe the position of the exhibits; $i$-th of these lines contains three integers $x_i$, $y_i$, $v_i$ ($-10^9 \leq x_i, y_i \leq 10^9$, $1 \leq v_i \leq 10^9$) indicating that the $i$-th exhibit has a value of $v_i$ bytecoins and is located at the point $(x_i,y_i)$. Subsequent $m$ lines describe the guard positions, analogically. (However, $v_i$ denotes the amount, in bytecoins, to be paid by Bytemon to bribe $i$-th guard.) At each point there can be at most one guard or exhibit.
Output
Your program should output a single line containing a single integer indicating the maximum profit, in bytecoins, that could be achieved by Bytemon.
Examples
Input
5 3 2 3 2 6 2 5 1 3 5 5 8 7 3 4 8 6 1 3 8 3 4 3 5 5 7 6
Output
6
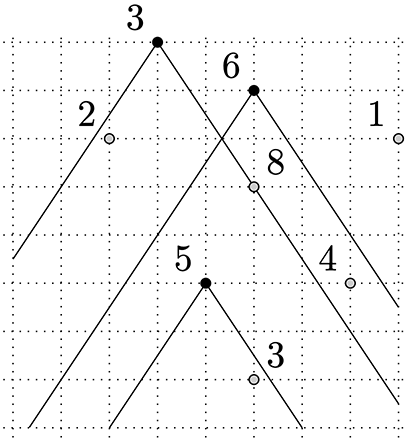
Angle of vision of each of the guards slightly exceeds $67^\circ$. Bytemon should bribe two guards, paying $3+6$ bytecoins, and take exhibits of a value of $2+8+4+1$ bytecoins.