A certain city has been coping with subway construction for a long time. The finances have been mismanaged and the costs have been underestimated to such extent that no funds were foreseen for the purchase of trains. As a result, too many stations and only some of the planned tunnels have been built - barely enough to allow a connection between any two stations to exist. The number of tunnels (each of them is bidirectional) is one less than the number of stations built. From the remaining funds only a handful of trains have been acquired.
To save their face, the board of directors have asked you to plan subway routes in such a way as to allow maximal number of stations to be connected. Each train travels on a specified route. The routes cannot branch (no three tunnels starting at a single station may belong to the same route). Distinct routes may comprise the same station or tunnel.
Write a programme which:
- reads a description of the tunnel system and the number of subway lines, which are to be planned from the standard input,
- calculates the maximal number of stations which can be covered by the specified number of subway lines,
- writes the outcome to the standard output.
Input
The first line of the standard input contains two integers $n$ and $l$ ($2 ≤ n ≤ 1\,000\,000$, $0 ≤ l ≤ n$) separated by a single space. $n$ denotes the number of stations and $l$ denotes the number of subway lines, which are to be planned. The stations are numbered from $1$ to $n$.
Each of the following $n-1$ lines contains two distinct integers separated by a single space. The numbers $1 ≤ a_i,b_i ≤ n$ in the $(i+1)$’th line denote the numbers of stations connected by $i$’th tunnel.
Output
The first and only line of the standard output should contain a single integer denoting the maximal number of stations which can be covered by train routes.
Example
Input
17 3 1 2 3 2 2 4 5 2 5 6 5 8 7 8 9 8 5 10 10 13 13 14 10 12 12 11 15 17 15 16 15 10
Output
13
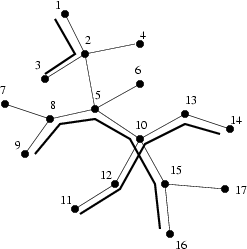
The figure represents the tunnel system (with subway routes marked) in one of the optimal configurations.