有一块 $n$ 行 $m$ 列的网格板,$n, m$ 都是奇数。网格上平铺着一些 $1\times2$ 的积木。积木可以旋转,不能重叠。这些积木共有 $\frac{nm-1}{2}$ 块,也就是说,网格板上只有一格的空位。
你可以做两种操作:
- 将一块与空白格相邻(指有公共边)的积木旋转 $90^\circ$ 到空白格中;
- 将一块与空白格相邻的积木平移至空白格中。
如图所示(被移动的积木颜色较浅):
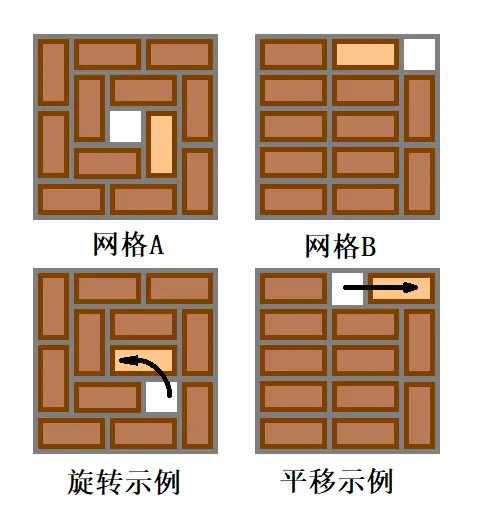
请你用以上两种操作将给定的网格板变换为指定的状态。
输入格式
第一行两个正奇数 $n, m$,分别表示网格的行数和列数。
接下来 $n$ 行,每行 $m$ 个字符,描述网格板的初始状态:
<表示这个格子是一块积木的左半部分;>表示这个格子是一块积木的右半部分;n表示这个格子是一块积木的上半部分;u表示这个格子是一块积木的下半部分;o表示这个格子是空的。
接下来另外 $n$ 行,每行 $m$ 个字符,描述你需要将网格板变成的目标状态,格式同上。
输出格式
你需要输出一个字符串,按顺序表示你的操作:
L表示你移动了空白格左侧的积木;R表示你移动了空白格右侧的积木;U表示你移动了空白格上方的积木;D表示你移动了空白格下方的积木。
当然,没有操作的话输出空串就好了。
样例数据
样例 1 输入
3 3 nnn uuu o<> <>n <>u <>o
样例 1 输出
URLR
样例 2 输入
5 5 n<><> un<>n nuonu u<>un <><>u <><>o <><>n <><>u <><>n <><>u
样例 2 输出
RLLRLRR
样例 2 解释
初始状态和目标状态分别是题图中的网格 $A,B$。
子任务
你输出的操作序列长度不能超过 $8\times10^6$。
对于所有数据,$1\le n, m\le 2000$。
- 对于 $10\%$ 的数据,$n,m\le 3$;
- 对于另外 $10\%$ 的数据,$n,m \le 5$;
- 对于另外 $20\%$ 的数据,$m=3$;
- 对于另外 $20\%$ 的数据,$n,m \le 50$;
- 对于另外 $20\%$ 的数据,$n,m \le 200$;
- 对于余下 $20\%$ 的数据,无特殊限制。