In the computer game Mega Jump, the hero jumps between peaks of a mountain range in order to reach the point with a flag, where the level ends.
The mountain range in the game consists of $n$ consecutive peaks; the $i$-th peak is located at position $i$ and has height $h_i$. For any $i < j$, the hero can jump in a straight line from peak $i$ to peak $j$, provided that during the straight-line flight there are no other peaks on his path. More formally, there must not exist an index $k$ such that $i < k < j$ and the вершина of the $k$-th peak—the point with coordinates $(k, h_k)$—lies strictly above the segment connecting the points $(i, h_i)$ and $(j, h_j)$.
The company Defeat AI is training a neural network to control the hero in this game. To create training data, it is necessary to answer several queries: for a pair of indices $l, r$ ($1 \le l \le r \le n$), determine the minimum number of jumps such that, starting at the peak with index $l$, the hero can reach the peak with index $r$.
Input Format
The first line of the input contains an integer $n$ ($1 \le n \le 10^5$) — the number of peaks.
The second line contains $n$ numbers: $h_1, h_2, \ldots, h_n$ ($0 \le h_i \le 10^{12}$) — the heights of the peaks.
The third line contains an integer $q$ ($1 \le q \le 10^5$) — the number of queries.
Each of the next $q$ lines contains two integers $l_i, r_i$ ($1 \le l_i \le r_i \le n$) — the parameters of the corresponding query.
Output Format
For each query, output on a separate line a non-negative integer — the minimum required number of jumps.
Scoring
| Subtask | Points | Additional Constraints | Required Subtasks |
|---|---|---|---|
| 1 | 9 | $n, q \le 300$ | — |
| 2 | 9 | $n, q \le 5000$ | 1 |
| 3 | 14 | $h_i \le 10$ | — |
| 4 | 21 | There exists $k$ such that for all $i$ it holds that $l_i \le k \le r_i$ | — |
| 5 | 27 | $n, q \le 5 \cdot 10^4$ | 1, 2 |
| 6 | 20 | — | 1–5 |
Example
standard input
8 5 3 4 3 6 2 1 4 3 1 8 2 7 4 4
standard output
2 2 0
Note
Let us consider the second query from the example. The hero’s path from peak 2 to peak 7 may look as follows:
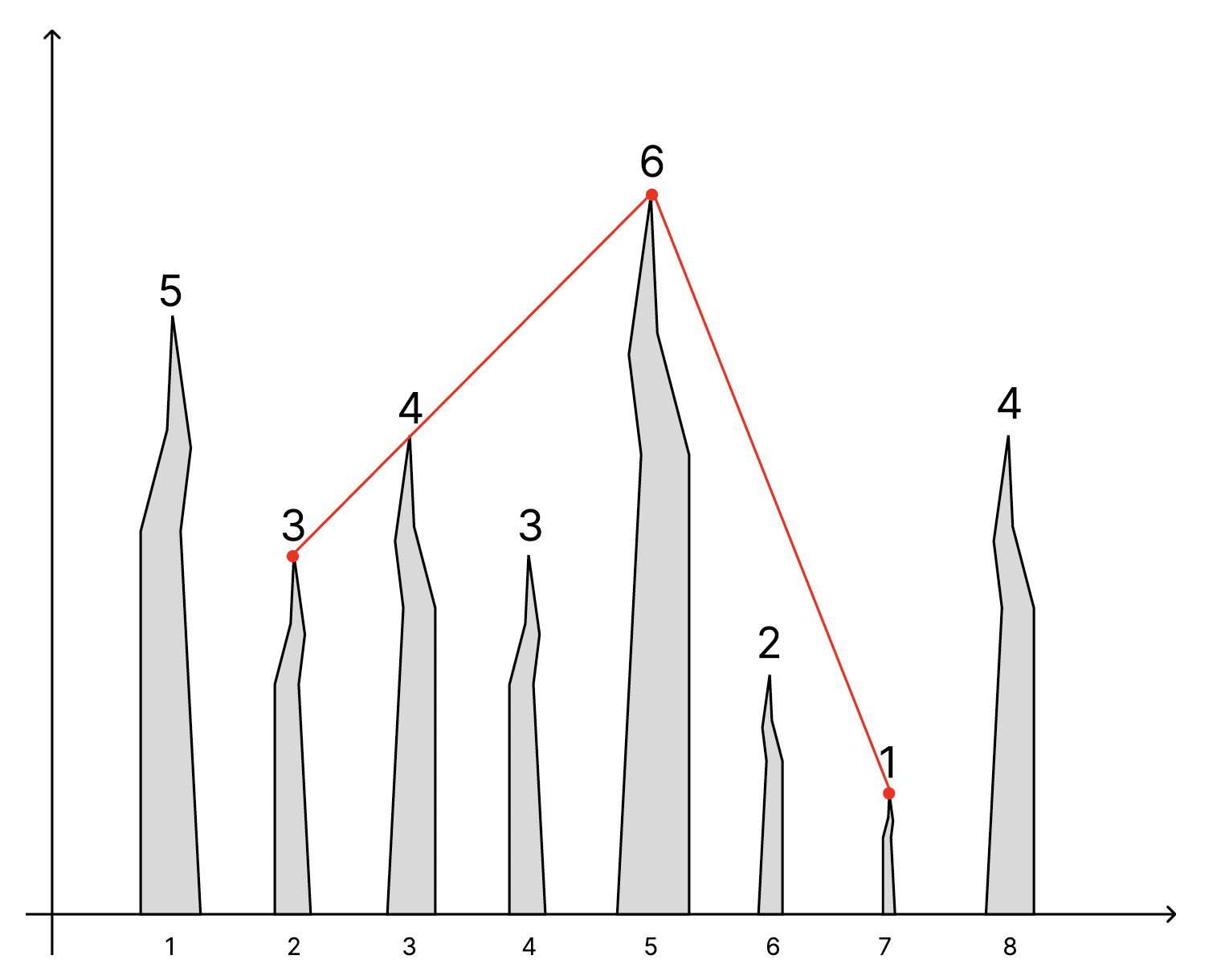
He will visit peaks 2, 5, and 7, making two jumps.