题目描述
有一个 $n\times m$ 的网格,你希望用带编号的3-联通块(triomino,即俄罗斯方块中的那种联通块,3-长条形或L形)覆盖整个网格。这些3-联通块需要使用 $1$ 到 $nm/3$ 编号。另外,如果两个3-联通块 $X$、$Y$ 满足 $X$ 中存在任意一个格子处于 $Y$ 中某个格子的正左方或正上方,则必须有 $X$ 的编号小于 $Y$ 的编号。
你需要输出(带编号的)覆盖方案数,对 $10^9+7$ 取模。有多组数据。
输入格式
第一行正整数 $T$,表示数据组数。
接下来 $T$ 行每行两个正整数 $n,m$。
输出格式
$T$ 行一行一个答案。
样例数据
样例输入
3
1 2
3 4
9 10样例输出
0
12
983018242样例解释
对于样例中的第二组数据,所有方案如下图:
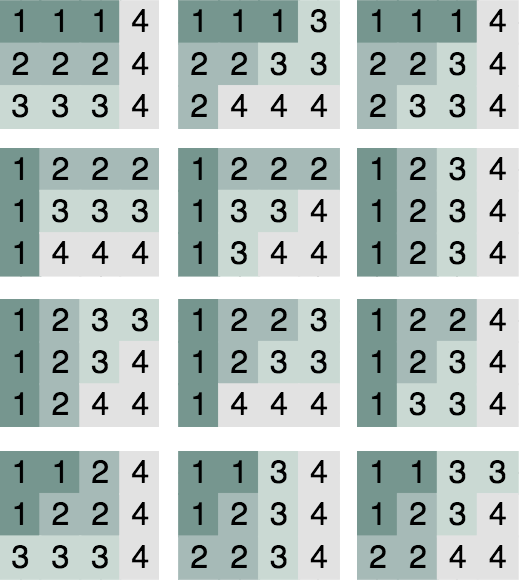
数据范围
对于所有数据,$T\le 10$,$n,m\le 10^4$。
Subtask 1(10pts):$n,m\le 4$。
Subtask 2(30pts):$n\le 4$,$m\le 100$。
Subtask 3(20pts):$n,m\le 100$。
Subtask 4(40pts):无特殊限制。