正二十面体(regular icosahedron) 总共有 $20$ 个面,$12$ 个顶点,$30$ 条棱。这是一张示意图。
岐艾拿到了一个正二十面体,她将每个面都用 $3n-3$ 刀切割成了 $n^2$ 个彼此全等的等边三角形。例如下图是一个 $n=2$ 的情况。
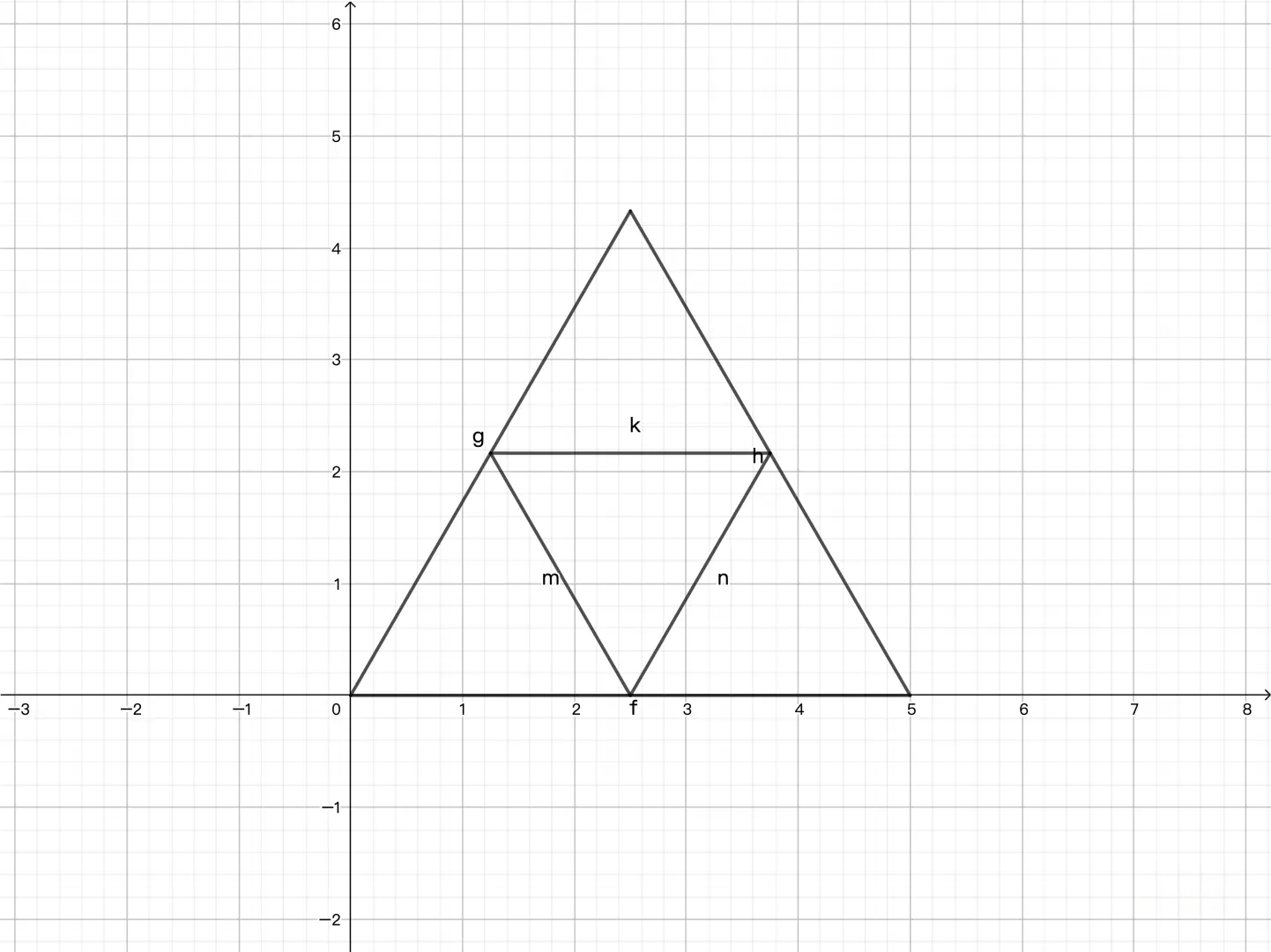
现在这个正 $20$ 面体总共有了 $20n^2$ 个小三角形,岐艾有 $k$ 种颜色。她希望将这些三角形进行涂色使得有 $a_i$ 个三角形涂上了第 $i$ 种颜色。
此外,即使是同种颜色,其颜料的价格也有所不同。对于第 $i$ 种颜色,有价格为 $0,1,\dots,b_i$ 的颜料各一种。一种价格为 $c$ 的颜料的意思是说用它每涂一个格子就要花费 $c$ 元钱。对于同种颜色,也可以在涂色方案中任意地使用不同价格的颜料。
岐艾现在有 $m$ 元钱的预算,所以她想知道对于每个 $0\le j\le m$,她有多少种方案恰好花 $j$ 元钱。
如果两种染色方案能够通过旋转这个正二十面体变成相同,则视为一种方案。注意:由于岐艾很专业,每个格子上所涂颜料的价格也是可以被她分辨出来的。
输入格式
第一行输入三个正整数 $n,m,k$。
接下来 $k$ 行每行两个整数 $a_i,b_i$。
输出格式
输出一个整数,设 $j$ 元钱对应的方案数是 $f(j)$,那么你只需要输出
$$ \bigoplus_{j=0}^m ((f(j) \bmod 998244353) + j) $$
样例数据
样例 1 输入
1 100 1 20 1
样例 1 输出
3554
样例 1 解释
解码前的数据有:
$$ f(0,\dots,10) = [1, 1, 6, 21, 96, 262, 681, 1302, 2157, 2806, 3158] $$
并且 $f(j)=f(20-j)$,$j>20$ 的部分均有 $f(j)=0$。
样例 2 输入
1 100 2 9 3 11 2
样例 2 输出
870
样例 3 输入
2 100 2 36 3 44 2
样例 3 输出
788814413
样例 4 输入
2 100000 2 36 233 44 666
样例 4 输出
953441426
数据范围
对于 $100\%$ 的数据,保证
- $1\le n\le 7\times 10^3$
- $0\le m\le 5\times 10^6$
- $1\le k\le 5$
- $1\le a_i$
- $\sum_i a_i = 20n^2$
- $0\le b_i\le m$
| 数据点编号 | 特殊限制 |
|---|---|
| $1$ | $n=1,k=1$ |
| $2$ | $n=1$ |
| $3,4$ | $b_i=0$ |
| $5\sim 8$ | $m=10^5$ |
| $9\sim 12$ | $n\leq 500$ |
| $13\sim 16$ | $a_i=20n^2/k$ |
| $17\sim 20$ | 无 |