This is a harder version of Counting Cactus from 300iq Contest 2.
NEERC featured a number of problems about cactuses: connected undirected graphs in which every edge belongs to at most one simple cycle. Intuitively, a cactus is a generalization of a tree where some cycles are allowed. An example of a cactus from NEERC 2007 problem is given on the picture below.
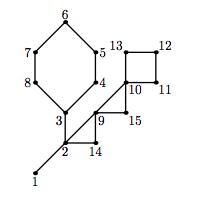
Dreamoon has an undirected graph. Now he is wondering, how many subgraphs (subsets of edges) of his graph are cactuses? Can you help him find this value modulo $998\,244\,353$?
Input
The first line contains two integers $n$ and $m$: the number of vertices and edges in the Dreamoon's graph ($1 \le n \leq {\color{red}{\mathbf{18}}}$, $0 \leq m \leq \frac{n(n-1)}{2}$).
The next $m$ lines describe edges in the graph. The $i$-th of these lines contains two integers $a_i$ and $b_i$ ($1 \le a_i, b_i \le n$, $a_i \neq b_i$), denoting an edge between vertices $a_i$ and $b_i$. It is guaranteed that there are no multiple edges.
Output
Output one integer: the number of cactus subgraphs of Dreamoon's graph, modulo $998\,244\,353$.
Examples
Input
3 3 1 2 2 3 3 1
Output
4
Input
5 0
Output
0
Input
8 9 1 5 1 8 2 4 2 8 3 4 3 6 4 7 5 7 6 8
Output
35
Notes
- $1\le n\le {\color{red}{\mathbf{18}}}$
- $0\le m\le \frac{n(n-1)}2$
- $u\neq v, 1\le u, v\le n$; there are no multiple edges.
Subtasks:
- ($16$ points) $n\le 5$
- ($20$ points) $n\le 7$
- ($14$ points) $n\le 10$
- ($20$ points) $n\le 13$
- ($10$ points) $n\le 16$
- ($20$ points) No additional constraints