Byteasar lives in Byteburg, a city famous for its milk bars on every corner. One day Byteasar came up with an idea of a "milk multidrink": he wants to visit each milk bar for a drink exactly once. Ideally, Byteasar would like to come up with a route such that the next bar is always no further than two blocks (precisely: intersections) away from the previous one.
The intersections in Byteburg are numbered from to , and all the streets are bidirectional. Between each pair of intersections there is a unique direct route, ie, one that does not visit any intersection twice. Byteasar begins at the intersection no. and finishes at the intersection no. .
Your task is to find any route that satisfies Byteasar's requirements if such a route exists.
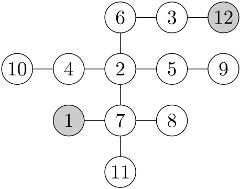
An exemplary route satisfying the requirements is: 1,11,8,7,5,9,2,10,4,6,3,12.
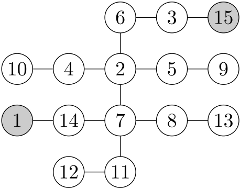
There is no route that satisfies the requirements.
Input Format
In the first line of the standard input there is a single integer $n$ ($2 ≤ n ≤ 500\,000$), denoting the number of intersections in Byteburg. Each of the following $n-1$ lines holds a pair of distinct integers $a_{i}$ and $b_{i}$ ($1 ≤ a_{i},b_{i} ≤ n$), separated by a single space, that represent the street linking the intersections no. $a_{i}$ and $b_{i}$.
Output Format
If there is no route satisfying Byteasar's requirements, your program should print a single word "BRAK" (Polish for none), without the quotation marks to the standard output. Otherwise, your program should print $n$ lines to the standard output, the i-th of which should contain the number of the i-th intersection on an arbitrary route satisfying Byteasar's requirements. Obviously, in that case the first line should hold the number $1$, and the $n$-th line - number $n$.
Example
Input
12 1 7 7 8 7 11 7 2 2 4 4 10 2 5 5 9 2 6 3 6 3 12
Output
1 11 8 7 4 10 2 9 5 6 3 12
Input 2
15 1 14 14 7 7 8 7 11 7 2 2 4 4 10 2 5 5 9 2 6 3 6 3 15 11 12 8 13
Output 2
BRAK