A rectangle $n \times m$ grid has $nm$ cells. There are $2d$ cells of them which contain numbers $1,1,2,2,$...$,d,d$. These cells are guaranteed to be on the border of the grid (i.e., at $1$-st row or $n$-th row or $1$-st column or $m$-th column).
You need to draw $d$ paths to connect these $d$ pairs of cells with the same number. Every path is a polyline consisting of several horizontal and/or vertical segments. The paths cannot go out of the grid. The $i$-th path should start at the center-point of a cell containing number $i$, and stop at the center-point of the other cell with number $i$. The path can go straight, or turn left/right at the center-point of a cell. The path should never go through a cell more than once. Moreover, two different paths cannot have common points, i.e., they should never go through the same cell. It is allowed that some cells are never passed through by any path.
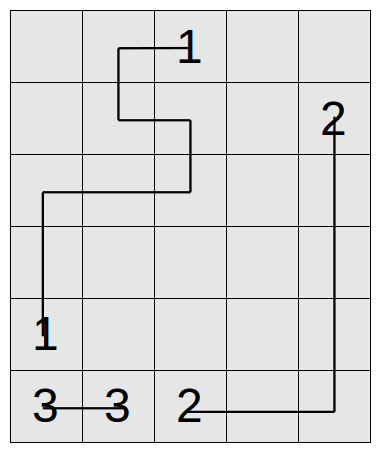
Given the grid, you need to construct a valid drawing, or report that it is impossible.
Input
The input will consist of several test cases.
In each test case, the first line contains three integers $n,m,d$. ($1\leq n,m\leq 2000$, $d\ge 1$)
Then $d$ lines follow. The $i$-th line of them contains four integers $x_1,y_1,x_2,y_2$ ($1\leq x_1,x_2\leq n$, and $1\leq y_1,y_2\leq m$), meaning that the coordinates of the two cells containing number $i$ are $(x_1,y_1)$ and $(x_2,y_2)$. These $2d$ cells are distinct and are guaranteed to be on the border of the grid. The top-left cell of the grid has coordinate $(1,1)$ and the bottom-right cell has coordinate $(n,m)$.
There are at most $50000$ test cases. Over all test cases, the sum of $nm$ is at most $4\times 10^7$.
Output
For each test case, if it is impossible to draw, only print "Impossible" in one line. Otherwise, print "Possible" in the first line, and then output $n$ lines, each with $m$ characters, denoting your constructed drawing. The format is described as follows.
For a cell containing a number, use '<', '>', '^', 'v' (go left, go right, go up, go down, respectively) to denote the direction of the path starting from this cell.
For a cell being passed through, use '7', 'L', 'r', 'J', '-', '|' (left-down, right-up, right-down, left-up, left-right, up-down, respectively) to denote how the path goes through this cell.
For other cells, print '.'.
There can be multiple possible drawings. You may output any of them.
Example
Input
6 5 3 5 1 1 3 6 3 2 5 6 2 6 1 3 3 4 1 1 2 1 1 2 3 3 1 3 2 3 3 1 3 2
Output
Possible .r<.. .L7.v r-J.| |...| ^...| ><>-J Impossible