Anton 想收到一张大小为 $n\times m$ 的矩形表格作为礼物,表格中填有数字 0、1、2、3 或 4。
如果满足以下条件,Anton 会很开心:每个 “0” 周围没有其他 “0”;每个 “1” 周围恰好有一个 “1”;每个 “2” 周围恰好有两个 “2”;每个 “3” 周围恰好有三个 “3”;每个 “4” 周围恰好有四个 “4”(也就是说,所有与 “4” 相邻的格子也都必须是 “4”)。
如果两个格子共享一条边,则认为它们是相邻的。
你需要设计一个表格作为礼物送给 Anton,使得他会感到开心。
下面是一个在 $n=4, m=6$ 时能让 Anton 开心的表格示例。
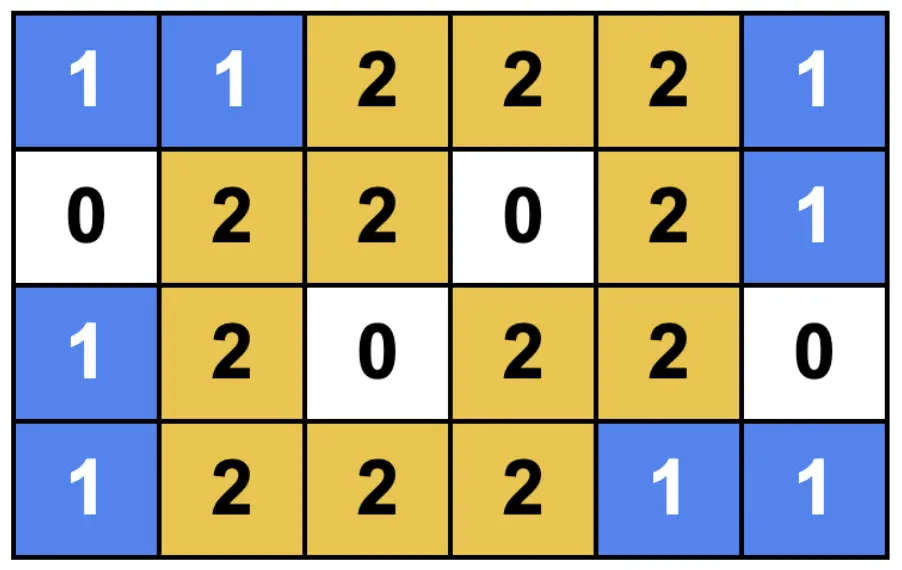
输入
一行包含两个整数 $n, m$ ($1 \leq n, m \leq 200$) --- 表格的尺寸。
可以证明,总是存在一种可行解。
输出
输出一个 $n$ 行 $m$ 列的表格 --- 作为送给 Anton 的礼物。
示例
输入
4 6
输出
1 1 2 2 2 1 0 2 2 0 2 1 1 2 0 2 2 0 1 2 2 2 1 1
评分
- ($10$ 分):$n = 1$;
- ($10$ 分):$n = 2$;
- ($10$ 分):$n = 3$;
- ($10$ 分):$n = m = 4$;
- ($10$ 分):$n = m = 30$;
- ($5$ 分):$n = 30, m = 31$;
- ($5$ 分):$n = 30, m = 32$;
- ($10$ 分):$n = m = 31$;
- ($5$ 分):$n = 31, m = 32$;
- ($10$ 分):$n = m = 32$;
- ($15$ 分):无额外限制。