For a pair of points on the Cartesian plane $(x_1, y_1)$ and $(x_2, y_2)$, we define the Manhattan distance between them as $|x_1-x_2|+|y_1-y_2|$. For example, for the pair of points $(4, 1)$ and $(2, 7)$, the Manhattan distance between them is $|4-2|+|1-7| = 2+6 = 8$.
You are given $2 \cdot n$ points on the Cartesian plane, whose coordinates are integers. All $y$-coordinates of the given points are either $0$ or $1$.
Split the given points into $n$ pairs such that each of these points belongs to exactly one pair, and the maximum Manhattan distance between the points of one pair is minimized.
Input
The first line contains a single integer $n$ $(1 \le n \le 10^5)$.
In the following $2 \cdot n$ lines, each line contains two integers $x_i$ and $y_i$ $(0 \le x_i \le 10^9, 0 \le y_i \le 1)$~--- the coordinates of the corresponding point.
Output
Output a single integer~--- the maximum Manhattan distance between the points of one pair in the optimal partition.
Example
Input
1 3 1 1 0
Output
3
Input
3 18 0 3 0 1 0 10 0 8 0 14 0
Output
4
Input
4 3 0 0 1 5 0 2 1 6 0 3 0 5 1 2 1
Output
2
Notes
In the second example, the pairing $[(18, 0), (14, 0)]$, $[(3, 0), (1, 0)]$, and $[(8, 0), (10, 0)]$ is the only optimal partition. The Manhattan distances between the points of one pair in this partition are $4$, $2$, and $2$, respectively.
In the third example, the pairing $[(0, 1), (2, 1)]$, $[(2, 1), (3, 0)]$, $[(3, 0), (5, 0)]$, and $[(5, 1), (6, 0)]$ is an optimal partition. All Manhattan distances between the points of one pair in this partition are equal to $2$.
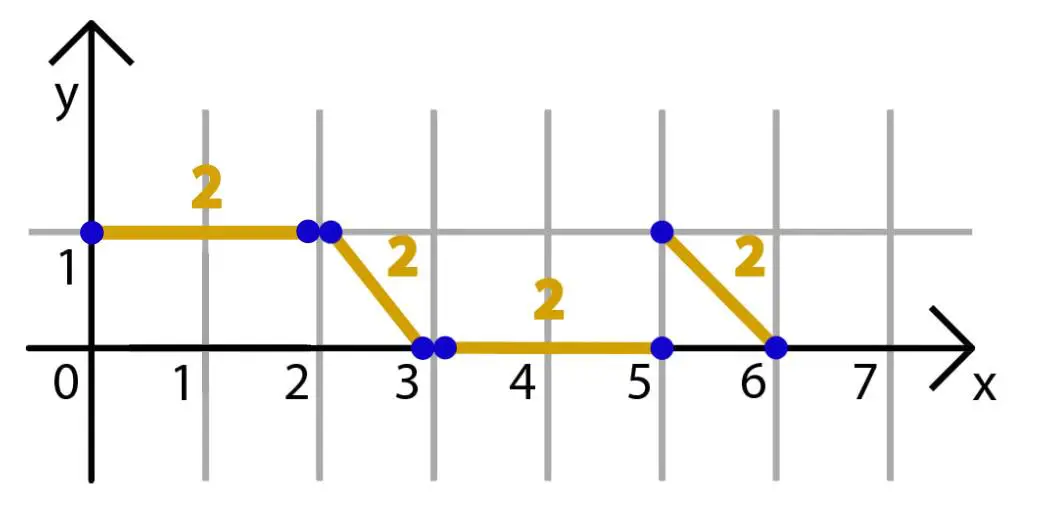
Illustration for the third example
Scoring
- ($2$ points): $n = 1$;
- ($3$ points): $x_i = 0$ for $1 \le i \le 2\cdot n$;
- ($4$ points): $n \le 4$;
- ($11$ points): $n \le 10$;
- ($14$ points): $y_i = 0$ for $1 \le i \le 2\cdot n$;
- ($10$ points): $x_i \neq x_j$ for $1 \le i < j \le 2\cdot n$;
- ($29$ points): $n \le 1000$;
- ($27$ points): no additional restrictions.