有 $n$ 个非负整数 $a_1, a_2, \ldots, a_n$ 按照圆形排列。按照圆形顺序,相邻的数字是 $a_1$ 和 $a_2$,$a_2$ 和 $a_3$,$\ldots$,$a_{n-1}$ 和 $a_n$,$a_n$ 和 $a_1$。
将这些数字划分为三个非空组,使得每个数字恰好属于一个组,每组中的数字在圆形中是连续排列的,并且三组中数字总和的最大值与最小值之间的差值最小。
输入
第一行包含一个整数 $n$ $(3 \le n \le 10^6)$ —— 被排列的数字数量。
第二行包含 $n$ 个非负整数 $a_1, a_2, \ldots, a_n$ $(0 \le a_i \le 10^9)$ —— 按圆形排列的数字。
输出
第一行输出一个整数 —— 在最优划分中,三组数字总和的最大值与最小值之间的差值。
第二行输出三个整数 $x$, $y$, $z$ $(1 \le x < y < z \le n)$ ~--- 这些索引使得最优划分的三组形式为 $[a_{x}, a_{x+1}, \ldots, a_{y-1}]$,$[a_{y}, a_{y+1}, \ldots, a_{z-1}]$,$[a_{z}, a_{z+1}, \ldots, a_{n-1}, a_{n}, a_{1}, a_{2}, \ldots, a_{x-1}]$。
如果有多个正确答案,输出任意一个都可以。
示例
输入
4 1 2 3 4
输出
1 1 3 4
输入
7 1 6 1 0 5 3 2
输出
0 2 3 6
输入
8 3 1 4 1 5 9 2 6
输出
1 3 6 8
说明
在第三个示例中,最优划分如下所示:
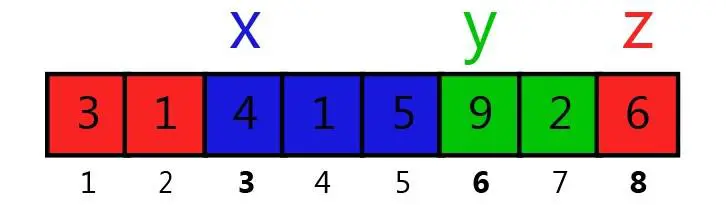
此时三组的和为 $10$, $11$, 和 $10$。
评分
1.($2$ 分):$n = 3$;
2.($4$ 分):对所有 $1 \le i \le n$ 有 $a_i \le 1$;
3.($13$ 分):存在一个划分使得差值为 $0$;
4.($8$ 分):$n \le 100$;
5.($9$ 分):$n \le 2000$;
6.($13$ 分):$n \le 5000$;
7.($28$ 分):$n \le 10^5$;
8.($23$ 分):无其他额外限制。