По колу розставлені $n$ невід'ємних цілих чисел $a_1, a_2, \ldots, a_n$. Сусідніми в порядку по колу є числа $a_1$ та $a_2$, $a_2$ та $a_3$, $\ldots$, $a_{n-1}$ та $a_n$, $a_n$ та $a_1$.
Розбийте ці числа на три непорожні групи так, щоб кожне число належало рівно одній групі, числа з однієї групи були розташовані послідовно по колу, а різниця між максимальною та мінімальною сумами чисел у групах була мінімально можливою.
Вхідні дані
У першому рядку задано одне ціле число $n$ $(3 \le n \le 10^6)$ -- кількість розставлених чисел.
У другому рядку задано $n$ невід'ємних цілих чисел $a_1, a_2, \ldots, a_n$ $(0 \le a_i \le 10^9)$ -- розставлені по колу числа.
Вихідні дані
У першому рядку виведіть одне ціле число~--- різницю між максимальною та мінімальною сумами чисел у групах в оптимальному розбитті.
У другому рядку виведіть три цілі числа $x$, $y$, $z$ $(1 \le x < y < z \le n)$~--- такі номери, що оптимальне розбиття чисел на три групи має вигляд $[a_{x}, a_{x+1}, \ldots, a_{y-1}]$, $[a_{y}, a_{y+1}, \ldots, a_{z-1}]$, $[a_{z}, a_{z+1}, \ldots, a_{n-1}, a_{n}, a_{1}, a_{2}, \ldots, a_{x-1}]$.
Якщо існує кілька правильних відповідей, дозволяється вивести будь-яку з них.
Приклади
Вхідні дані
4 1 2 3 4
Відповідь
1 1 3 4
Вхідні дані
7 1 6 1 0 5 3 2
Відповідь
0 2 3 6
Вхідні дані
8 3 1 4 1 5 9 2 6
Відповідь
1 3 6 8
Примітка
У третьому прикладі оптимальне розбиття виглядає наступним чином:
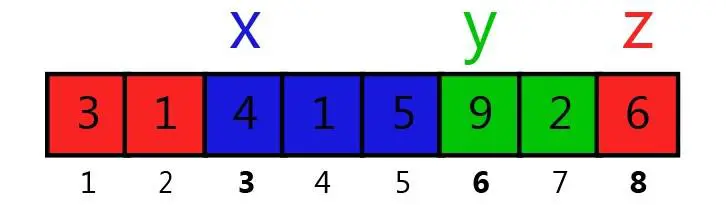
У такому випадку суми в групах дорівнюють $10$, $11$ і $10$.
Оцінювання
- ($2$ бали): $n = 3$;
- ($4$ бали): $a_i \le 1$ для $1 \le i \le n$;
- ($13$ балів): існує розбиття, де шукана різниця рівна $0$;
- ($8$ балів): $n \le 100$;
- ($9$ балів): $n \le 2000$;
- ($13$ балів): $n \le 5000$;
- ($28$ балів): $n \le 10^5$;
- ($23$ бали): без додаткових обмежень.