On an extremely large chess board many chessmen were located^{1} - all of them of the same colour. We say that a given chessman can capture specified position on the chess board, if the chessman can move to that position, particularly:
- there is no chessman standing on destination position,
- there are no chessmen on the way from the initial position to the destination (in case of a queen, a rook and a bishop).
No chessman can capture the position on which it is standing. Notice that a single position can be captured by multiple chessmen.
Write a program which:
- reads a description of the chessboard from the standard input,
- for each chessman determines the number of positions being captured by that chessman,
- writes the result to the standard output.
^{1}You can read more about chess and chessmen here: http://en.wikipedia.org/wiki/Chess_piece.
Input Format
In the first line of the input there are two integers $ n $ and $ m $ ($1 ≤ n ≤ 200\,000$, $1 ≤ m ≤ 10^{9}$), separated with a single space and representing the number of chessmen located on the square chessboard and its dimension $ m $. Each of the $ n $ following lines is of the format "$ F $ $ x $ $ y $", where $ F $ is a letter representing:
G- bishop,H- queen,K- king,S- knight,W- rook,
and $(x, y)$ is a location of the chessman ($1 \le x, y \le m$). No two chessmen are located in the same position.
Output Format
The output should consist of $ n $ lines. $ i $'th line should contain one integer, representing the number of positions being captured by $ i $'th chessman from the input.
Example
Input
6 5 K 5 5 G 4 1 W 1 3 K 2 3 H 2 2 S 3 3
Output
3 2 4 5 7 7
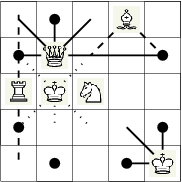
The image above represents the chessboard from the sample input. Lines of different style represent positions being captured by chessmen. The possible destinations of the knight are represented by big dots.