In Byteland there are $ n $ cities numbered from 1 to $ n $. These cities are connected by a network of $ m $ bidirectional roads. It is known that each pair of cities is connected by at most one road.
Byteman admitted recently that he likes some cities more than others. More precisely, he spends his time especially well in cities with numbers from 1 to $ k $, so during every journey he visits each of them at least once.
Byteman's journey is a sequence of $ d $ cities, such that each pair of consecutive cities is connected by a road. The journey can start and end in any city. Your task is to compute the number of distinct journeys around Byteland that Byteman can make. Because this number might be quite large, it will be enough to find it modulo $10^{9} + 9$.
Write a program that:
- reads a description of the network of connections in Byteland from the standard input,
- computes remainder of the division of the number of distinct journeys that can be made by $10^{9} + 9$,
- writes the result to the standard output.
Input Format
The first line of input contains four integers $ n $, $ m $, $ k $ and $ d $ ($1 ≤ n ≤ 20$, $1 ≤ k ≤ \min(n, 7)$, $1 ≤ d ≤ 1\,000\,000\,000$), separated by single spaces. The following $ m $ lines contain descriptions of connections between cities of Byteland. A description of a road consists of two numbers $ a_{i} $, $ b_{i} $ ($1 ≤ a_{i}, b_{i} ≤ n $, $ a_{i} ≠ b_{i} $), separated by a single space and denoting the numbers of cities connected by the $ i $'th road.
Output Format
The output should contain one integer, denoting the number of distinct journeys that Byteman can make, modulo $10^{9} + 9$.
Example
Input
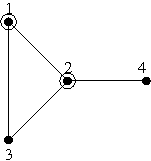
4 4 2 3 1 2 2 3 3 1 2 4
Output
10
All possible Byteman's journeys are:
- 1 → 2 → 1
- 1 → 2 → 3
- 1 → 2 → 4
- 1 → 3 → 2
- 2 → 1 → 2
- 2 → 1 → 3
- 2 → 3 → 1
- 3 → 1 → 2
- 3 → 2 → 1
- 4 → 2 → 1