We are given a regular polygon with $ n $ vertices. Let's choose $ m $ of its diagonals. We would like to know if there is such a pair of diagonals that intersect (having a common end-point does not count as intersection).
Write a program which:
- reads a description of the polygon and selected diagonals from the standard input,
- checks whether there is a pair of diagonals that intersect,
- writes the result to the standard output.
Input Format
In the first line of the input there are two integers $ n $ and $ m $ ($4 ≤ n ≤ 1\,000\,000$, $2 ≤ m ≤ 10\,000\,000$), separated with a single space and representing the number of vertices of the polygon and the number of selected diagonals. Following $ m $ lines contain descriptions of diagonals. Each line contains two integers $ a_{i} $ and $ b_{i} $ ($1 ≤ a_{i}, b_{i} ≤ n$), separated with a single space and representing diagonal, which joins vertex number $ a_{i} $ with vertex number $ b_{i} $ (polygon's vertices are numbered with natural numbers from $1$ to $n$ in a counter-clockwise manner). You can assume that each pair of numbers defining a single diagonal defines a valid diagonal (not a single vertex or polygon's edge). All diagonals in the input will be different.
Output Format
The first and only line of the output should contain:
- one word
NIE(i.e. no in Polish), if there is no pair of diagonals that intersect, or - two different integers $ p $ and $ q $ ($1 ≤ p, q ≤ m $, $ p ≠ q $), separated with a single space and representing numbers of diagonals that intersect. In case of multiple correct answers, your program can output any one of them. Diagonals are numbered in order of occurrence in the input.
Example
Input
6 4 3 6 1 4 6 2 2 5
Output
2 3
Input 2
6 2 1 3 1 5
Output 2
NIE
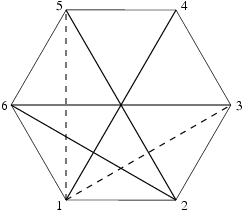
In the image above, solid lines represent diagonals from the first input, while stroked lines represent diagonals from the second input.