A number from 1 to n is inscribed in each cell of a $2 \times n$ grid in such a way that each number appears exactly twice in the grid and each column contains two different numbers. An example of such a configuration is depicted below.
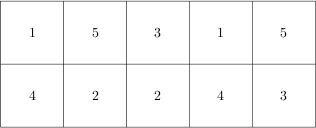
We would like to colour each of the cells white or gray in such a way that cells located in the same column receive different colours and cells containing same number receive different colours. An example of such a colouring of the grid from the previous figure is depicted below.
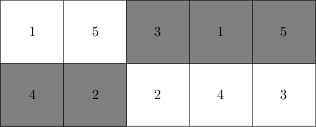
How many such colourings exist?
Input Format
The first line of the standard input contains one integer $n$ ($2 ≤ n ≤ 100$). Each of the following two lines contains n integers in the range $[1, n]$, separated by single spaces. The numbers in these lines represent numbers inscribed in consecutive cells of the grid.
Output Format
The first and only line of the standard output should contain a single integer - the number of different colourings of the grid with two colours that fulfill the described conditions.
Example
Input
5 1 5 3 1 5 4 2 2 4 3
Output
4
Please note that the example describes the grid from the above figures.