Sędziwy Bajtazar jest właścicielem sadu, w którym rosną jabłonie wydające szczerozłote owoce. Niestety, praca w sadzie jest ciężka, a Bajtazar nie ma już tyle sił co dawniej, postanowił więc podzielić swój sad na działki, które da do uprawy swoim synom. Bajtazar chciałby zapewnić każdemu z synów dostatnie życie, więc pragnie, aby każdemu z nich przypadła w udziale co najmniej jedna drogocenna jabłoń.
Sad Bajtazara ma kształt prostokąta o wymiarach $ n \times n $ metrów. Dla uproszczenia wprowadzamy w nim prostokątny układ współrzędnych, w którym lewy dolny róg sadu ma współrzędne $(0, 0)$, a prawy górny róg - współrzędne $(n, n)$. Wiemy, w których kwadratach jednostkowych sadu rosną jabłonie. Działki powstałe w wyniku podziału sadu powinny być prostokątami o bokach zawartych w liniach siatki układu współrzędnych. Działki nie mogą na siebie nachodzić - mogą jedynie stykać się bokami lub wierzchołkami - i muszą pokrywać cały sad. Wymiary działek nie mają znaczenia; istotne jest tylko to, aby każda działka zawierała przynajmniej jedną jabłoń.
Możesz założyć, że żądany podział sadu jest możliwy.
Input Format
Pierwszy wiersz wejścia zawiera dwie liczby całkowite $ n $ oraz $ k $ ($1 \le n \le 1\,000$, $1 \le k \le n^{2}$) oznaczające długość boku sadu oraz liczbę synów Bajtazara. Kolejne $ n $ wierszy zawiera opis zawartości poszczególnych kwadratów sadu. Każdy z tych wierszy zawiera $ n $ znaków x i/lub . oznaczających odpowiednio kwadrat zawierający i niezawierający jabłoni.
Output Format
Twój program powinien wypisać na wyjście $ k $ wierszy opisujących przykładowy podział sadu na działki. Każdy z wierszy powinien zawierać cztery liczby całkowite $ x_{1}$, $ y_{1} $, $ x_{2} $, $ y_{2} $ oznaczające współrzędne lewego dolnego $(x_{1}, y_{1})$ i prawego górnego $( x_{2}, y_{2})$ wierzchołka działki. Kolejność, w jakiej działki zostaną podane na wyjściu, nie ma znaczenia - już Bajtazar będzie wiedział, którą działkę przydzielić któremu synowi.
Example
Input
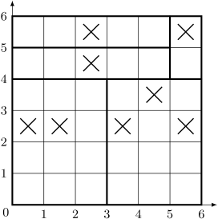
6 5 ..x..x ..x... ....x. xx.x.x ...... ......
Output
0 0 3 4 0 4 5 5 5 4 6 6 3 0 6 4 0 5 5 6