Bajtazar 买了一把剪刀。现在他想测试一下,于是拿起了附近的一个多边形,打算把它切割成若干个矩形。他决定要用尽可能少的切割次数来完成这件事。请帮助 Bajtazar 计算他需要进行多少次切割。
这个多边形只由垂直和水平的线段组成。在动手剪之前,Bajtazar 会在多边形上画出一些垂直或水平的线段。每一条线段的起点和终点都在多边形的边界上,而线段的内部则完全位于多边形内部。然后,Bajtazar 会沿着这些画好的线段切开多边形。切割次数即为画线段的数量。所有切割完成后,得到的所有部分都应该是矩形。
请注意,进行若干次切割后,有些画好的线段可能已经被先前的切割分成了几段,但如果沿着一条画好的线段的所有碎片都切割完成,这些都只算作一次切割。特别地,这意味着一个 $2 \times 2$ 的正方形可以仅用两刀分成四个 $1 \times 1$ 的小正方形(当然,从 Bajtazar 的目标来看,这样切割其实没什么意义)。
输入格式
输入的第一行包含一个整数 $n$($4 \le n \le 100,000$),表示多边形的顶点数。接下来的 $n$ 行描述了多边形的各个顶点。第 $i$ 个顶点由两个整数 $x_{i}$, $y_{i}$($-10^{9} \le x_{i}, y_{i} \le 10^{9}$)给出,表示该顶点的坐标。
所有多边形的边都为垂直或水平。仅当两条边在多边形边界上是相邻的两条边时,它们才可能相交,并且此时它们的交点只有公共顶点一个点。特别地,所有顶点的坐标都是两两不同的。
输出格式
你的程序应输出将该多边形切分成矩形所需的最少切割次数。
示例
输入
8 0 0 6 0 6 7 4 7 4 3 2 3 2 5 0 5
输出
2
说明
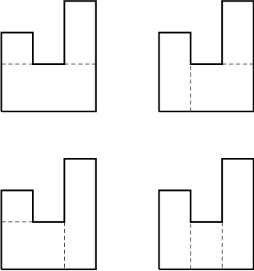
上图展示了用两刀将样例中的多边形切成矩形的几种可能方案。