Nadszedł czas, by znowu pomalować mieszkanie. Bajtazar nie przepada za malowaniem, jednak zauważył, że pojemniki z farbą i pędzle wzbudziły żywe zainteresowanie wśród jego dzieci. Rozdał więc pędzle dzieciom i poprosił je o pomalowanie jednej ze ścian. Każde z dzieci pomalowało fragment w kształcie prostokąta o bokach równoległych lub prostopadłych do podłogi.
Niestety okazało się, że farba zakupiona przez Bajtazara nie jest najlepszej jakości, przez co dobrze wyglądają teraz jedynie te fragmenty ściany, które zostały pominięte przez co najwyżej jedno dziecko. Jaka jest łączna powierzchnia tych fragmentów?
Input Format
W pierwszym wierszu wejścia znajduje się liczba całkowita $ n $ ($2 \le n \le 500\,000$), oznaczająca liczbę dzieci Bajtazara.
Każdy z kolejnych $ n $ wierszy opisuje obszar zamalowany przez jedno dziecko. W $ i $-tym spośród tych wierszy znajdują się cztery liczby całkowite $ x_{1}$, $ y_{1} $, $ x_{2} $, $ y_{2}$ ($0 \le x_{1} < x_{2} \le 10^{9}$, $0 \le y_{1} < y_{2} \le 10^{9}$). Oznaczają one, że $ i $-te dziecko pomalowało obszar będący prostokątem, którego lewy dolny wierzchołek leży w punkcie $(x_{1}, y_{1})$, prawy górny wierzchołek leży w punkcie $(x_{2}, y_{2})$, a boki są równoległe do osi układu współrzędnych.
Output Format
Twój program powinien wypisać na wyjście jedną liczbę całkowitą - powierzchnię tej części ściany, która nie wymaga dalszego malowania, to znaczy została pomalowana przez co najmniej $ n - 1$ dzieci.
Example
Input
3 0 0 5 5 1 0 2 5 0 1 6 3
Output
13
Notes
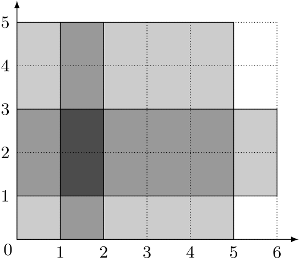
Do wyniku wliczają się obszary zamalowane na rysunku ciemniejszym i najciemniejszym kolorem.