Bajtazar kupuje meble przez Internet. Znalazł już ładny stół i zestaw krzeseł. Teraz zastanawia się, ile krzeseł może kupić, tak aby wszystkie zmieściły się przy stole.
Stół ma prostokątny blat o wymiarach $ A \times B $ centymetrów. Z kolei siedzisko krzesła, patrząc z góry, to kwadrat o wymiarach $ K \times K $ centymetrów. Dalej będziemy traktować stół jako prostokąt, a krzesła - jako kwadraty.
Nad jednym z brzegów siedziska (kwadratu) znajduje się oparcie. Każde krzesło należy ustawić oparciem przy stole, tzn. brzeg z oparciem powinien pokrywać się z pewnym brzegiem stołu. Ponadto siedzisko powinno w całości znajdować się pod blatem. Oczywiście żadne dwa krzesła nie mogą na siebie nachodzić. W naszych rozważaniach pomijamy nogi od stołu (możemy założyć, że są nieskończenie cienkie i znajdują się w rogach blatu). Ile krzeseł zmieści się pod stołem?
Input Format
W jedynym wierszu wejścia znajdują się trzy liczby całkowite $ A $, $ B $ i $ K $ ($1 \le A , B , K \le 500\,000\,000$) oznaczające, odpowiednio, wymiary blatu stołu oraz wymiar siedziska krzesła.
Output Format
Twój program powinien wypisać na wyjście maksymalną liczbę krzeseł, które zmieszczą się przy stole.
Example
Input
15 18 4
Output
10
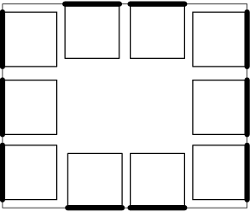
Rysunek pokazuje przykładowe rozmieszczenie krzeseł przy stole. Oparcia zostały zaznaczone pogrubionymi odcinkami. Nie jest możliwe ustawienie jedenastu krzeseł.
Input 2
12 8 4
Output 2
6