A tree is an undirected graph in which any two nodes are connected with at most one simple path, that is, a path without repeating nodes.
Consider a tree with $n$ nodes numbered $1$ through $n$. Let $P$ be a permutation of the set of nodes of the tree, that is, a one-to-one function (injection) $P : \{1, 2, \ldots, n\} \to \{1, 2, \ldots, n\}$. The permutation P is called an automorphism if for any two nodes $u$, $v$ of the tree, the nodes $P(u)$ and $P(v)$ are connected with an edge if and only if $u$ and $v$ are connected with an edge.
We would like to know what is the number of different automorphisms of a given tree modulo $1\,000\,000\,007$.
Input Format
The first line of the standard input contains an integer $n$ ($1 ≤ n ≤ 500,000$): the number of nodes of the tree. Each of the following n-1 lines contains two integers $u_{i}$ and $v_{i}$ ($1 ≤ u_{i} < v_{i} ≤ n$) that represent an edge connecting the nodes $u_{i}$ and $v_{i}$.
Output Format
The first and only line of the standard output should contain one integer: the number of different automorphisms of the given tree modulo $1\,000\,000\,007$.
Example
Input
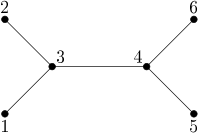
6 1 3 2 3 3 4 4 5 4 6
Output
8
Notes
This tree has 8 automorphisms, in particular, the following three:
$p(i) = i$ for $i = 1, 2, 3, 4, 5, 6$
$q(i) = i$ for $i = 1, 2, 3, 4, q(5) = 6, q(6) = 5$
$r(1) = 6, r(2) = 5, r(3) = 4, r(4) = 3, r(5) = 1, r(6) = 2$.