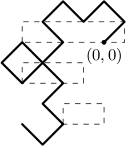Byteasar 仍然在玩他的绘图仪,并打印字节曲线(参见题目 Plotter)。 (回顾一下,阶数为 $n$ 的字节曲线由 $2^n$ 条长度为 $\sqrt{2}$ 的线段组成,第一条线段连接点 $(0, 0)$ 和 $(1, 1)$,而在任意两条相邻线段之间,画笔都会转向 90°:第 $i$ 次转向($1 \le i < 2^n$)是向右转,当且仅当 $i = 2^k(1+2l)$,其中 $k$ 是非负整数,$l$ 是奇数。)
Byteasar 发现他可以用绘图仪画出漂亮的轨迹。为此,在启动绘图仪之前,他会将一条纸胶带贴在纸上,覆盖一个矩形区域,该矩形的对角顶点为坐标 $(x_1, y)$ 和 $(x_2, y+1)$。在绘图仪完成绘图之后,Byteasar 会撕下胶带,欣赏其上的精美轨迹。
一条 轨迹 指的是一段在胶带上绘制的、长度为正的连通曲线。
在等待绘图仪完成的过程中,Byteasar 想知道:在胶带上将会画出多少条轨迹?你能帮他回答这个问题吗?
输入格式
标准输入的第一行包含两个整数 $n$ 和 $m$($1 \le n, m \le 2000$),分别表示字节曲线的阶数和询问的数量。接下来的 $m$ 行,每行包含三个整数 $x_1$、$x_2$ 和 $y$($-10^9 \le x_1 < x_2 \le 10^9$,$-10^9 \le y \le 10^9$),描述每次粘贴胶带所覆盖的矩形。
输出格式
你的程序应输出 $m$ 行,每行一个整数,表示对应询问中胶带上绘制的轨迹数。
示例
输入
4 3 -4 1 0 -4 -1 -2 -2 0 -4
输出
2 1 0
(可参考下图所示)