Note: Some inputs have extra tokens at the end.
WWT大爷是一个魔法师,最近他盯上了OI中的线段树这个数据结构,并且正在对它进行改造。
在普通的线段树当中,对于一个区间$[l,r]$,我们会选择$mid= \lfloor \frac{l+r}{2} \rfloor$,将该区间分成$[l,mid],[mid+1,r]$。它们在树上则对应的节点是原区间对应的节点的左右儿子。
魔法师WWT使用了高位魔法将此规则打破,在他的线段树里,他可以自己选择$mid$的值(但$mid$依然满足$l \leq mid < r$),以至于使得线段树的深度超过原来的限制$O(logn)$,以及区间定位时间复杂度超过原来的限制$O(logn)$。但其余条件基本同原OI中的线段树。
如下图,是一棵mid任意的线段树:

*什么是区间定位:
用最少的线段树上节点表示的线段去拟合这个区间,使得每个单位长度有且仅在这些线段中出现一次。
如上面这棵线段树,线段[2,5]的区间定位是[2,3],[4,4],[5,5],共三个。
我们也不难证明这样的区间定位是唯一的。魔法师WWT不仅使用了高位魔法打破了线段树的基本法,还使用了一些禁忌魔法修改了这个线段树的结构。他将指定树中的某个子结构进行左旋或者右旋的操作。如下图所示:
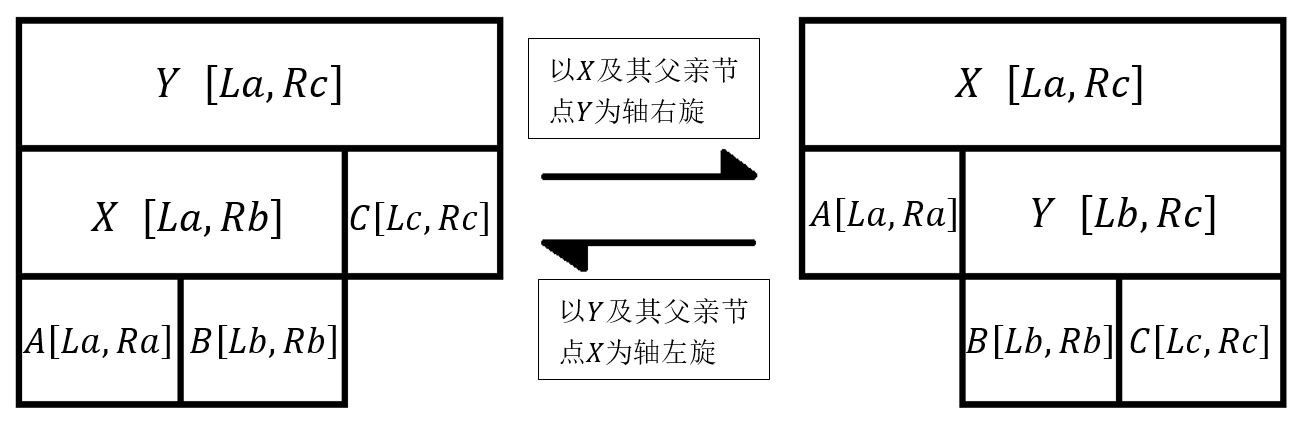
不难发现该旋转规则同Splay的旋转模式类似。
①子树A,B,C不会产生任何变化。
②子树A,B,C及节点X,Y之间的相对位置会发生改变。
③节点X,Y的区间刻度会发生改变。魔法师WWT会给你一棵$mid$值任意的线段树,在对这棵树的某些节点进行旋转的同时,询问你某个区间在当前线段树上的区间定位个数。
WWT觉得这样一道题还不能足以体现他高超的魔法水平,于是他又对某些数据进行了加密,使选手们的算法强制在线。
输入格式
第一行包括三个整数$N,Q,type$,分别代表线段树的宽度,操作个数,以及该数据是否加密。若$type=0$,表示这个数据没有进行加密,若$type=1$,表示这个数据进行了加密。
以下N-1行以先序遍历(深度优先顺序)描述一棵线段树,每行一个正整数表示当前非叶子节点的$mid$,保证每个节点$l \leq mid < r$。同时,我们将所有非叶子节点按照先序遍历标号,从$1$ ~ $N-1$。
读入时建议选手直接采用递归,走到叶子节点时回溯即可,所以一共N-1个mid,而且保证1~N-1各出现一次。
此后$Q$行每行代表一个操作。
每行的第一个整数$tp$,代表该操作的类型:
若$tp=0$,则代表一个修改操作,该行还包括一个正整数$x'$,记$lastans$为上一次询问的答案,若之前没有询问操作,则$lastans=0$,我们定义$x=x' \oplus (type \times lastans)$。$x$表示该旋转操作的儿子节点编号,你需要以$x$以及$x$的父亲节点为轴进行一次旋转操作,若$x$是它父亲的左儿子则进行一次右旋,若$x$是它父亲的右儿子则进行一次左旋。WWT对自己的魔法过于自信,以至于有时他给的非叶子结点$x$是当前线段树的根的编号,这是一个非法的修改操作,此时你需要输出一行 "BAD!",并且不对当前的线段树进行任何操作
若$tp=1$,则代表一个询问操作,该行还包括两个正整数$l',r'$,记$lastans$为上一次询问的答案,若之前没有询问操作,则$lastans=0$,我们依次定义$l=l' \oplus (type \times lastans),r=r' \oplus (type \times lastans)$。则$[l,r]$表示该询问操作中的询问区间,对于每次询问,你需要给出在当前线段树上该区间的区间定位个数。
输出格式
输出包括若干行: 对于一个非法的修改操作,输出一行 "BAD!"; 对于一个询问操作,输出一个正整数,表示答案。
对于一个合法的修改操作不需要输出。
样例输入
7 12 1 4 3 1 2 5 6 1 3 6 1 6 3 1 1 5 0 7 1 7 2 1 6 3 1 0 4 0 0 1 0 5 1 6 3 1 3 7 0 0
样例输出
4 3 4 4 2 3 4 1 3 BAD!
样例解释
样例解密之后:
7 12 0 4 3 1 2 5 6 1 3 6 1 2 7 1 2 6 0 3 1 3 6 1 2 7 1 2 6 0 3 1 3 6 1 2 7 1 2 6 0 3
线段树初始形状如下:

$1:[3,6]$的区间定位是$[3,3],[4,4],[5,5],[6,6]$,共$4$个。
$2:[2,7]$的区间定位是$[2,3],[4,4],[5,7]$,共$3$个。
$3:[2,6]$的区间定位是$[2,3],[4,4],[5,5],[6,6]$,共$4$个。
$4:$ 以3及其父亲2为轴进行右旋,右旋后形状如下。

$5:[3,6]$的区间定位是$[3,3],[4,4],[5,5],[6,6]$,共$4$个。
$6:[2,7]$的区间定位是$[2,4],[5,7]$,共$2$个。
$7:[2,6]$的区间定位是$[2,4],[5,5],[6,6]$,共$3$个。
$8:$ 以3及其父亲1为轴进行右旋,右旋后形状如下。
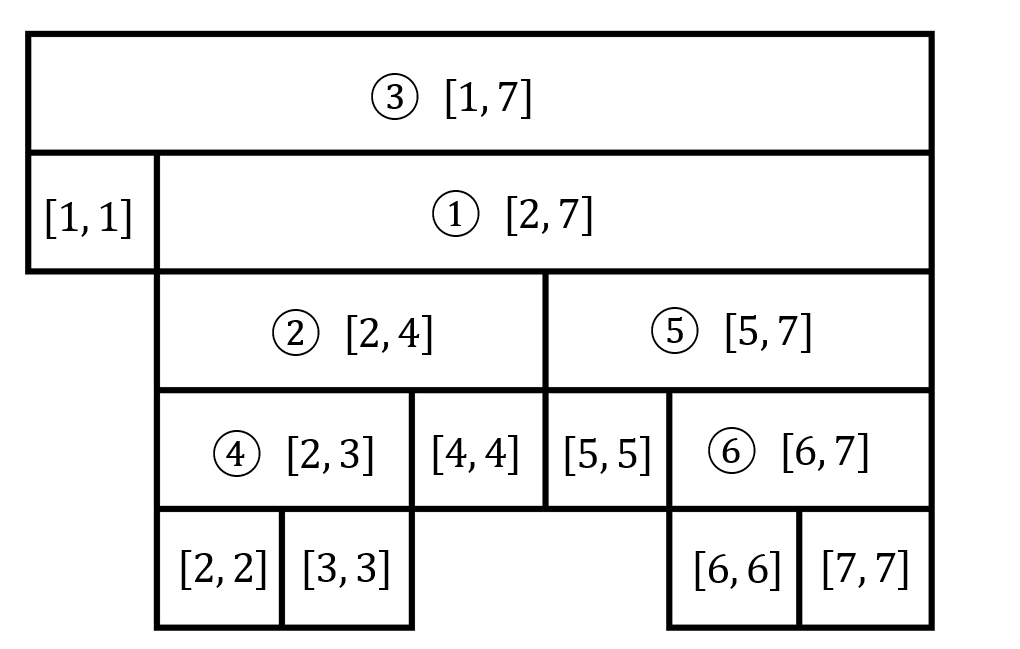
$9:[3,6]$的区间定位是$[3,3],[4,4],[5,5],[6,6]$,共$4$个。
$10:[2,7]$的区间定位是$[2,4],[5,7]$,共$2$个。
$11:[2,6]$的区间定位是$[2,4],[5,5],[6,6]$,共$3$个。
$12:$ 3号点已经是当前的根,非法的修改操作,输出“BAD!"。
数据范围
在所有的数据中,对于解密后的$l,r,x$,满足$1 \leq l \leq r \leq N, 1 \leq x \leq N-1$。
| 测试点编号 | N的大小不超过 | Q的大小不超过 | Type的值 | 是否有修改操作 | 空间限制 |
|---|---|---|---|---|---|
| 1 | 1000 | 1000 | 0 | 无 | 512MB |
| 2 | 1 | ||||
| 3 | 0 | 有 | |||
| 4 | 1 | ||||
| 5 | 200000 | 200000 | 0 | 无 | |
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | 1 | ||||
| 10 | |||||
| 11 | |||||
| 12 | 0 | 有 | |||
| 13 | 64MB | ||||
| 14 | 16MB | ||||
| 15 | 1 | 512MB | |||
| 16 | |||||
| 17 | 64MB | ||||
| 18 | |||||
| 19 | 16MB | ||||
| 20 |