Nobilul Stegan, un prinț al Dendromarcei, a rămas trist după moartea tatălui său. După multe încercări zadarnice de a afla soarta tatălui calculând aria diferitor trapeze folosind regula lui Simpson, un spirit i-a venit în ajutor. Spiritul i-a dat lui Stegan un arbore pentru a avea grijă de el. Spiritul i-a zis: _Uită-te! Mai aproape! Nu vezi? Acest arbore e special, deoarece are un număr par de vârfuri. Dacă vei găsi un mod de a împărți vârfurile în perechi astfel ca costul lor să fie cât mai mic posibil, tu vei afla cum ți-a murit tatăl. Dar mai întâi trebuie să îți dai seama care e costul unei perechi. Secretul ține de sensul vieții._
Stegan, fiind un matematician, știe că sensul vieții poate fi găsit în cuvintele: "To be xor not to be" ( frază care nu poate fi tradusă în limba română). El a dedus că pentru o pereche de vârfuri, costul perechii este valoarea operației $XOR$ (SAU exclusiv) pe biți pe greutățile muchiilor care se află pe drumul între aceste vârfuri.
În detrimentul lui Stegan, el e lipsit de abilități computaționale, de aceea te roagă pe tine să-l ajuți.
Formal, îți este dat un arbore cu $N$ vârfuri, $N$ fiind par. Fiecare muchie are o greutate. Pentru o pereche de vârfuri $(u,v)$ noi definim costul perechii ca valoarea operației $XOR$ (SAU exclusiv) pe biți pe greutățile muchiilor care se află pe drumul între aceste vârfuri.
Tu trebuie să găsești un mod de a împărți vârfurile în $\frac{N}{2}$ perechi astfel ca suma costurilor să fie cât mai mică posibilă. Deoarece poate fi dificil să aflați suma minimă a costurilor, noi vă rugăm doar să faceți cât de bine puteți, fiind punctați corespunzător.
Date de intrare
Prima linie de intrare conține un număr întreg par, $N$ - numărul de vârfuri în arbore. Următoarele $N−1$ linii conțin $3$ numere separate prin spațiu, $u_i, v_i, w_i,$ însemnând că vârfurile $u_i$ și $v_i$ sunt conectate printr-o muchie cu greutatea $w_i$.
Date de ieșire
Pe prima linie afișați suma costurilor perechilor de vârfuri pe care le-ai ales. Pe următoarele $\frac{N}{2}$ linii afișați indicii vârfurilor care formează fiecare pereche. Nicio pereche nu trebuie să conțină vârfuri în comun.
Punctare
Pentru fiecare grup:
- Dacă este un test pentru care depășești limita de timp sau primești Runtime Error, vei primi $0$ puncte pentru acel grup.
- Dacă este un test în care oricare din cele $\frac{N}{2}$ perechi afișate nu este validă sau suma costurilor nu corespunde cu valoarea afișată, vei primi $0$ puncte pentru acel grup.
- Dacă nici una din cele de sus nu se aplică, vei primi puncte după următoarea formulă:
$\displaystyle \text{group\_score} \cdot \text{min}\left\{ \left( \frac{ok\_cost_i}{out\_cost_i} \right) ^4\right\}$, unde:
- $i$ trece prin fiecare test din grup
- $out\_cost_i$ este răspunsul afișat pentru testul $i$
- $ok\_cost_i$ este răspunsul optim pentru testul $i$
Restricții și precizări
- $2 \leq N \leq 200$
- $N$ este par
- $0 \leq w_i \leq 2^{24}$
| # | Puncte | Restricții |
|---|---|---|
| 1 | 3 | $N \leq 10, w_i \leq 64$ |
| 2 | 6 | $N \leq 14$ |
| 3 | 19 | $N \leq 40, w_i \leq 64$ |
| 4 | 8 | $N \leq 120, w_i \leq 16$ |
| 5 | 41 | $N \leq 120$ |
| 6 | 23 | Fără restricții suplimentare. |
Exemplul 1
stdin
6 5 2 42 5 4 52 6 3 26 4 6 39 1 6 15
stdout
54 1 6 3 5 4 2
Explicație
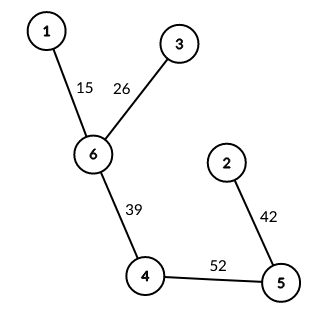
Exemplul 2
stdin
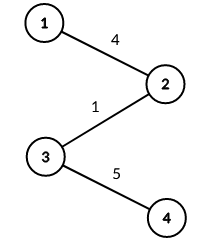
4 1 2 4 3 4 5 2 3 1
stdout
1 2 3 1 4
Explicație