Doi din cei mai neastâmpărați Daci din toată istoria, Danillo și Stegano, s-au gândit că ar fi amuzant să sape niște tunele care nu duc nicăieri. Ei știau că viitorii istorici vor fi foarte confuzi în legătură cu existența unor tunele fără sens și vor încerca să găsească motivul construirii lor, când, de fapt, aceste tunele nu au niciun scop.
Aceștia au găsit un zid imens în care ar putea începe să sape, dar din păcate niște părți din zid sunt indestructibile, deci vor trebui să le ocolească. Din motive estetice, intrarea în tunel trebuie să fie circulară.
Mai exact, zidul poate fi descris ca un plan cartezian cu coordonatele $x$ în intervalul $[0,M]$ și coordonatele $y$ în intervalul $[0,N]$. Părțile care sunt indestructibile sunt pătrate cu laturile paralele cu axele, de lungime $1$ și cu colțurile în coordonate întregi. Harta zonelor ce pot fi săpate poate fi descrisă printr-o matrice binară cu $N$ linii numerotate de la $0$ la $N−1$ și $M$ coloane numerotate de la $0$ la $M−1$. Dacă elementul de pe linia $l$ și coloana $c$ este $1$, atunci toate punctele $(x,y)$ cu $c≤x≤c+1$ și $l≤y≤l+1$ pot fi săpate. Atenție la diferența între coordonatele $(x, y)$ în plan și coordonatele $(l, c)$ ca elemente ale matricei.
La săparea unui tunel, cei doi aleg un punct cu coordonate întregi $(x,y)$ ca și centru al tunelului, iar apoi ei aleg o rază $r$, și, în final, se apucă să sape prin toate punctele care se află în discul centrat în $(x,y)$ de rază $r$. Atenție la faptul că discul include toate punctele dinăuntrul lui, nu doar circumferința lui, și că discul trebuie să se afle complet înăuntrul planului definit.
Cerință
Aceștia își doresc ca tunelul lor să fie cât mai ușor de sesizat, așadar ei își doresc tunelul cu cea mai mare rază posibilă. Pentru o construire mai simplă, dacă există mai multe astfel de tunele, ei îl vor alege pe cel mai ușor de construit dintre ele. Dacă considerăm că centrul unui tunel este la coordonatele $(x,y)$, ei vor prefera tunelul cu cel mai mic $y$. Dacă încă există mai multe astfel de tunele, ei îl vor alege pe cel cu cel mai mic $x$ dintre acestea.
Date de intrare
Prima linie va conține două numere întregi $N$ și $M$ în această ordine, definind planul precum și mărimea matricei binare.
Următoarele $N$ linii conțin fiecare câte un șir binar de lungime $M$ format din $0$-uri și $1$-uri, reprezentând elementele matricei definite mai sus.
Date de ieșire
Afișați pe o singură linie trei numere întregi separate prin spații $x$, $y$ și $R$. $(x, y)$ reprezintă coordonatele centrului tunelului pe care Danillo și Stegano îl vor săpa, iar $R$ reprezintă raza cercului, ridicată la pătrat si aproximată la cel mai apropiat întreg. Dacă nu există vreun cerc care să aibă coordonate pozitive, se va afișa 0 0 0.
Restricții și precizări
- $1 \leq N, M \leq 3 \ 000$
| # | Puncte | Restricții |
|---|---|---|
| 0 | 0 | Exemplele |
| 1 | 4 | Matricea conține exact patru celule cu $1$. |
| 2 | 9 | Valorile de $1$ din matrice formează un dreptunghi cu laturile paralele cu axele. |
| 3 | 14 | $N, M \leq 50$ |
| 4 | 15 | $N, M \leq 600$ |
| 5 | 21 | Matricea este generată prin random. |
| 6 | 37 | Fără restricții suplimentare |
Exemplul 1
stdin
5 6 011110 111110 011111 111111 011110
stdout
3 2 4
Explicație
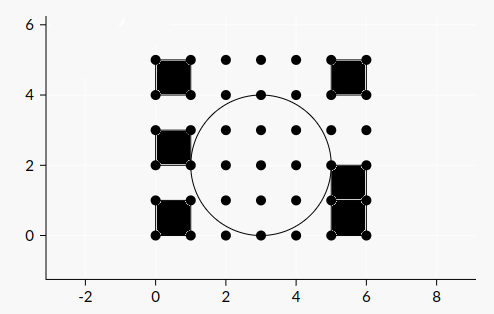
Exemplul 2
stdin
3 3 010 101 010
stdout
0 0 0