Un arbore AA este un arbore binar de căutare cu o structură specială. Fiecărui nod îi sunt atribuite o valoare și un nivel. Valorile îndeplinesc proprietățile obișnuite ale arborilor binari de căutare:
- Valoarea fiecărui fiu stâng (și a nodurilor din subarborele fiului stâng) este mai mică sau egală ca cea a tatălui său.
- Valoarea fiecărui fiu drept (și a nodurilor din subarborele fiului drept) este mai mare sau egală cu valoarea tatălui său.
Nivelele respectă următoarele reguli:
- Nivelul fiecărui nod frunză este $1$.
- Nivelul fiecărui fiu stâng este exact cu unu mai mic decât cel al tatălui său.
- Nivelul fiecărui fiu drept este egal sau cu unu mai mic decât cel al tatălui său.
- Nivelul fiecărui nepot drept este strict mai mic decât cel al bunicului său.
- Fiecare nod de nivel mai mare strict ca unu are exact doi fii.
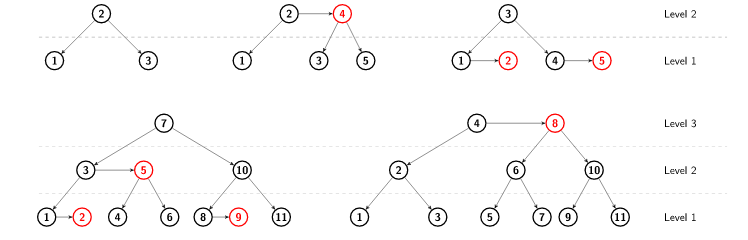
Mai jos găsiți cinci exemple de arbori AA, având $3$, $5$, $5$, $11$ și $11$ noduri. Pentru claritate, fiii drepți pe același nivel cu tații lor sunt colorați cu roșu.
Cerință
Date fiind două numere $N$ și $L$, câte moduri sunt de a aranja valorile $1$, $2$, ..., $N$ într-un arbore AA astfel încât acesta are fix $L$ nivele?
Date de intrare
Singura linie a datelor de intrare va conține numerele întregi $N$ și $L$ separate printr-un spațiu.
Date de ieșire
Afișați numărul de aranjări modulo $10^9 + 7$.
Restricții și precizări
- Enunțul problemei este puțin modificat din cauza unei erori în definiția arborilor binari de căutare în enunțul original al problemei.
- $1 \leq L \leq 9$
- $1 \leq N \leq 10 \ 000$
| # | Punctaj | Restricții |
|---|---|---|
| 0 | 0 | Exemplele |
| 1 | 19 | $L \leq 4$ |
| 2 | 34 | $5 \leq L \leq 7$ |
| 3 | 47 | Fără restricții suplimentare |
Exemplul 1
stdin
5 2
stdout
2
Explicație
Cele două posibile aranjări sunt arătate în imaginile $2$ și $3$ de mai sus.
Exemplul 2
stdin
442 6
stdout
896944318
Exemplul 3
stdin
7133 9
stdout
980381648