Bajtazar pracuje w przedsiębiorstwie zajmującym się produkcją kryształów. Każdy atom kryształu jest jednego z trzech rodzajów, które zwyczajowo oznacza się przez $ A_{0}, A_{1}, A_{2}$. Kryształ rzędu $ n $ składa się z $3n(n - 1) + 1$ atomów ułożonych w sześciokąt o boku $ n-1 $ składający się z $6( n - 1)^{2}$ równobocznych trójkątów o boku 1. Na poniższym rysunku znajduje się przykładowy kryształ rzędu 2:
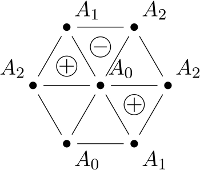
Kryształy wykazują się właściwościami elektrycznymi. Każde trzy atomy tworzące trójkąt o boku 1, które mają $ parami różne rodzaje $, wytwarzają pole elektryczne o jednostkowym ładunku - dodatnim, jeśli atomy znajdują się w kolejności $ A_{0}, A_{1}, A_{2}$, gdy obchodzimy trójkąt przeciwnie do ruchu wskazówek zegara, lub ujemnym, jeśli znajdują się w tej kolejności, gdy obchodzimy trójkąt zgodnie z ruchem wskazówek zegara. Ładunek całego kryształu jest równy sumie ładunków wszystkich trójek atomów.
Choć Bajtazar posiada urządzenie do produkcji dowolnie dużych kryształów, to działa ono dość osobliwie. Urządzenie programuje się, podając mu sześć liczb: $ n $, $ m $, $ s $, $ a $, $ b $, $ k $. Tworzy ono kryształ rzędu $ n $, ustawiając atomy wierszami, począwszy od najwyższego wiersza. W ramach każdego wiersza atomy są ustawiane od lewej do prawej. Rodzaj każdego kolejnego atomu $ A_{r} $ jest wybierany pseudolosowo przez zastosowanie następującej procedury:
$$ s := ((a \cdot s + b ) \operatorname{div} k) \bmod (3 \cdot m )$$
$$ r := s \operatorname{div} m $$
Operacja $ x $ div $ y $ oznacza tu część całkowitą z dzielenia $ x $ przez $ y $, zaś $ x $ mod $ y $ to reszta z dzielenia $ x $ przez $ y $. Powyższe dwie instrukcje wykonywane są jedna po drugiej.
Bajtazar poprosił Cię o napisanie programu, który wyznaczy ładunek kryształu dla zadanych parametrów wejściowych urządzenia.
Input Format
W pierwszym wierszu wejścia znajduje się sześć liczb całkowitych $ n $, $ m $, $ s $, $ a $, $ b $, $ k $ opisujących parametry wejściowe urządzenia do produkcji kryształów ($2 \le n \le 10^{9}$, $1 \le m \le 10^{6}$, $0 \le s, a, b < 3\cdot m$, $1 \le k < 3 \cdot m $).
Output Format
W jedynym wierszu wyjścia należy wypisać liczbę całkowitą oznaczającą ładunek kryształu, który zostanie wyprodukowany przez urządzenie dla zadanych parametrów.
Example
Input
2 7 0 5 10 1
Output
1